Flow-based Models and Flow Matching
An introduction to flow matching.
This is part one in a series of blog posts that will provide an introduction to flow-based models and flow matching.
Flow-based models are an example of a probabilistic generative model. The goal of probabilistic modeling is to model the distribution of a random variable \(X\). This is typically done in a supervised fashion using examples \(\{x^{(i)}\}_{i=1}^N\) collected from the data distribution. We learn to approximate the probability density function of the data distribution with a model \(p(x;\theta)\) where \(\theta\) represents the parameters of a neural network. Why might this be useful? The most well-known use case is sampling. Once we have an approximation of the data distribution, we can sample from it to create new unseen data. In the past decade, we have witnessed Variational Auto-Encoders (VAE), Generative Adversarial Networks (GAN) and diffusion models at the forefront of research in generative modelling. These models have been applied successfully across various domains especially for image generation.
Although flow-based models have recieved relatively less attention compared to other generative models in those years, there has been a recent surge in popularity due to the advent of flow matching. Flow matching encompasses diffusion models as a special case and offers a more simple and flexible training framework. We will build up to flow matching by covering some of the other relevant techniques developed for flow-based modeling in the past decade. Part one will start with normalizing flows and cover residual flow methods. Part two will touch on Neural ODEs and dicuss continuous normalizing flows. Finally, in part three, we dicuss flow matching and its generalizations such as Riemannian flow matching.
Other than being a competitive alternative to diffusion models, what are some other motivations to study flow-based methods and flow matching? Well, flow-based methods are capable of likelihood evaluation because they model the probability density function directly. Also, as we will see, the flow matching framework relies on Ordinary Differential Equations (ODE) so they are effecient at sample generation.
Normalizing Flows
In future blog posts, we will see that flow matching is a way to train continuous normalizing flows. So we start by covering the basics of normalizing flows. The framework for normalizing flows is based on a rather simple fact from probability theory. Suppose \(\mathbf{x_0} \in \mathbb{R}^d\) is distributed according to \(p\) i.e. \(\mathbf{x_0} \sim p\). Let \(f: \mathbb{R}^d \to \mathbb{R}^d\) be an invertible and differentiable function. Now, let’s do a change of variables, \(\mathbf{x_1} = f(\mathbf{x_0})\). Then we are able to determine \(q\), the distribution of the transformed variable, \(\mathbf{x_1}\), in terms of \(p\). Namely,
\[\begin{align} q(\mathbf{x_1}) &= p(\mathbf{x_0})\left|\det \frac{\partial f^{-1}}{\partial \mathbf{x_1}}(\mathbf{x_1})\right| \notag \\ &= p\left(f^{-1}(\mathbf{x_1})\right)\left|\det \frac{\partial f^{-1}}{\partial \mathbf{x_1}}(\mathbf{x_1})\right|. \end{align}\]The notation \(\frac{\partial f^{-1}}{\partial \mathbf{x_1}}\) denotes the Jacobian of \(f^{-1}\). Also, because the transformation is invertible, we can write \(p\) in terms of \(q\) too:
\[\begin{align*} p(\mathbf{x_0}) &= q(\mathbf{x_1})\left|\det \frac{\partial f}{\partial \mathbf{x_0}}(\mathbf{x_0}) \right| \\ &= q(f(\mathbf{x_0}))\left|\det \frac{\partial f}{\partial \mathbf{x_0}}(\mathbf{x_0}) \right|. \end{align*}\]Example 1 . Scaling and shifting a Gaussian. Suppose \(\mathbf{x_0} \in \mathbb{R}\) and \(\mathbf{x_0} \sim \mathcal{N}(0,1)\). Let \(\mathbf{x_1} = f(\mathbf{x_0}) = \sigma \mathbf{x_0} + \mathbf{\mu}\). Then \(\mathbf{x_0} = f^{-1}(\mathbf{x_1}) = \frac{\mathbf{x_1} - \mathbf{\mu}}{\sigma}\) so \(\frac{df^{-1}}{d\mathbf{x_1}} = \frac{1}{\sigma}\). In this case, the Jacobian is a positive scalar function so the determinant is itself. Recall the pdf of a canonical Gaussian:
\[p(\mathbf{x_0}) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}\mathbf{x_0}^2}.\]Applying the formula we obtain a Gaussian with mean \(\mu\) and variance \(\sigma^2\),
\[\begin{align*} q(\mathbf{x_1}) &= p\left(f^{-1}(\mathbf{x_1})\right)\left|\det \frac{\partial f^{-1}}{\partial \mathbf{x_1}}(\mathbf{x_1})\right| \\ &= \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x - \mathbf{\mu}}{\sigma})^2}\frac{1}{\sigma} \\ &= \frac{1}{\sqrt{2\pi\sigma}}e^\frac{-(x-\mathbf{\mu})^2}{2\sigma^2}. \end{align*}\]Intuitively, multiplying \(\mathbf{x_0}\) by \(\sigma\) stretches the domain which changes the variance of the Gaussian. Adding \(\mu\) applies a shift to this stretched Gaussian.
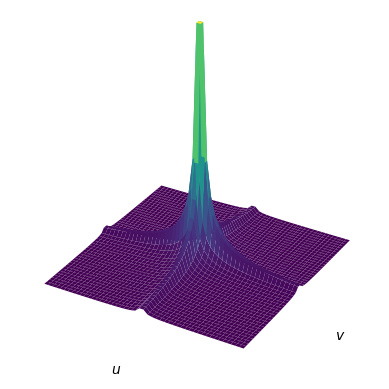
Example 2 . Non-linear transformation of a canonical Gaussian. Suppose \(\begin{bmatrix} x \\ y\end{bmatrix} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\). The pdf of a canonical Gaussian in 2D is:
\[p(x,y) = \frac{1}{\sqrt{2\pi}}e^\frac{-(x^2 + y^2)}{2}.\]Let’s apply a cubic transformation to each coordinate, \(u = x^3\) and \(v = y^3\). The inverse is \(x = u^\frac{1}{3}\) and \(y = v^\frac{1}{3}\). The Jacobian of this transformation is the following:
\[\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial v}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial v}{\partial v} \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{3}u^{-\frac{2}{3}} & 0 \\ 0 & \frac{1}{3}v^{-\frac{2}{3}}\\ \end{bmatrix}.\]The absolute value of the determinant of this matrix is \(\frac{1}{9}\lvert uv\rvert ^{-\frac{2}{3}}\). Therefore,
\[\begin{align*} q(u, v) &= \frac{1}{9}\lvert uv\rvert ^{-\frac{2}{3}} p(x,y) \\ &= \frac{1}{9}\lvert uv\rvert ^{-\frac{2}{3}}p(u^\frac{1}{3}, v^\frac{1}{3}) \\ &= \frac{\lvert uv\rvert ^{-\frac{2}{3}}}{9\sqrt{2\pi}}e^\frac{-(u^\frac{2}{3} + v^\frac{2}{3})}{2} \\ \end{align*}\]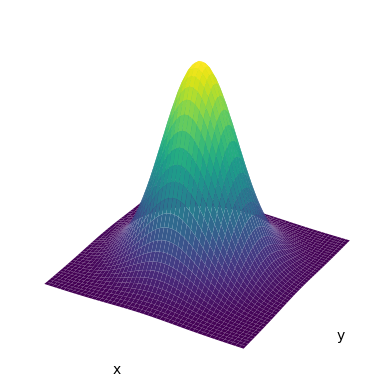
In the next sections, we will see that flow matching is capable of transforming between arbitrary distributions \(p\) and \(q\). But in the context of normalizing flows for generative modeling, \(p\) is simple distribution which we can sample from easily, typically a canonical Gaussian and \(q\) is our data distribution which we only have samples from i.e. the dataset \(x^{(i)}\). Our goal with this setup is to learn the transformation from \(p\) to the complex data distribution \(q\). We can do this by learning the invertible transformation \(f\). The function \(f\) will involve the use a neural network with parameters \(\theta\), so from now on we will denote the transformation as \(f_\theta\). Once we have learned \(f_\theta\) we will have access to \(\hat{q}\) which hopefully will be a good approximation of \(q\).
Given that we learned \(f_\theta\), how do we do density estimation and generate samples from \(q\)? This is quite simple for flow models. If you have a data sample \(\mathbf{x}^{(i)}\), you can compute \(f^{-1}(\mathbf{x}^{(i)})\) and the deterimant of the Jacobian. Then plug those into eq. (1) to obtain \(\hat{q}(\mathbf{x}^{(i)})\). If you want to sample from \(q\), first obtain a sample \(\mathbf{x_0} \sim p\) which we know how to do because \(p\) is a simple distribution. Then, we can compute \({\mathbf{x_1} = f^{-1}_\theta(\mathbf{x_0})}\) and so \(\mathbf{x_1}\) will be a sample from \(\hat{q}\). Essentially, normalizing flows provide a way to learn how to transform samples from a simple distribution to a complex data distribution. This might seem a bit neboulous right now. How do we learn the transformation \(f_\theta\) using only samples from the complex data distribution? First, we have to discuss how to determine the design of \(f_\theta\) and ensure that it is invertible.
Ensuring invertibility is challenging so normalizing flow methods start with imposing a specific structure on \(f_\theta\). We want to learn the transformation from \(p\) to \(q\) as a sequence of simpler transformations. Define functions \(f_1 \cdots f_k\) to be invertible and differentiable. Note these functions are still parameterized by \(\theta\) but we omit making this explicit for sake of notation. Invertible and differentiable functions are closed under composition. We can use this fact to define \(f_\theta\) in the following manner:
\[f_\theta = f_k \circ f_{k-1} \cdots f_2 \circ f_1.\]The intiution behind this formulation is somewhat analagous to the justification of stacking many layers in a deep learning model instead of using one wide layer. Learning the transformation from \(p\) to \(q\) in one step might be too difficult. Instead, we can learn a sequence of functions where each function is responsible for transforming its input distribution into a slightly more complex distribution. Eventually, over the entire sequence we are able to model the complexity of the data distribution. Furthermore, now we only need to ensure that each simpler transformation is invertible which should be easier than designing a complex invertible transformation in one step.

Let’s reformulate the process of normalizing flows. Since we are performing multiple steps, \(\mathbf{x_1}\) is no longer a sample from \(q\) but a sample from a distribution slightly more complex than \(p_0 = p\). After applying \(K\) transformations we will have that \(\mathbf{x_K} \sim \hat{q}\):
\[\begin{align*} &\phantom{\Rightarrow} \ \ \mathbf{x_0} \sim p_0, \quad \mathbf{x_1} = f_1(\mathbf{x_0}) \\ &\Rightarrow \mathbf{x_1} \sim p_1, \quad \mathbf{x_2} = f_2(\mathbf{x_1}) \\ \phantom{\Rightarrow x_1} &\cdots \\ &\Rightarrow \mathbf{x}_{K-1} \sim p_{K-1}, \quad \mathbf{x}_K = f_K(\mathbf{x}_{K-1}) \\ &\Rightarrow \mathbf{x}_K \sim p_K = \hat{q} \approx q. \end{align*}\]The sequence of transformations from \(p\) to the distribution \(q\) is called a flow. The term normalizing in normalizing flow refers to the fact that after a transformation is applied, the resulting pdf is valid i.e. it integrates to one over its support and is greater than zero.
So how do we actually train normalizing flows? The objective function is simply the maximum log-likelihood of the data:
\[\begin{align*} \theta^* &= \max_{\theta} \sum_{i=1}^{N} \log(\hat{q}(\mathbf{x}^{(i)})) \\ &= \max_{\theta} \sum_{i=1}^{N} \log\left(p\left(f^{-1}_\theta(\mathbf{x}^{(i)})\right)\left|\det \frac{\partial f^{-1}_\theta}{\partial \mathbf{x}_K}(\mathbf{x}^{(i)})\right|\right) \\ &= \max_{\theta} \sum_{i=1}^{N} \log p\left(f^{-1}_\theta(\mathbf{x}^{(i)})\right) + \log\left|\det \frac{\partial f^{-1}_\theta}{\partial \mathbf{x}_K}(\mathbf{x}^{(i)})\right| \end{align*}.\]Remember that \(f_\theta\) is actually the composition of a sequence of functions. We can simplify the determinant of the Jacobian of \(f\) by decomposing it as a product of the individual determinants. Specifically,
\[\left| \det \frac{f^{-1}_\theta}{\partial \mathbf{x}_K} \right| = \left| \det \prod_{k=1}^K \frac{f^{-1}_k}{\partial \mathbf{x}_k} \right| = \prod_{k=1}^K \left| \det \frac{f^{-1}_k}{\partial \mathbf{x}_k} \right|.\]Substituting this back into the objective function we obtain:
\[\max_{\theta} \sum_{i=1}^{N} \left[ \log p\left(f^{-1}_\theta(\mathbf{x}^{(i)})\right) + \sum_{k=1}^{K} \log\left|\det \frac{f^{-1}_k}{\partial \mathbf{x}_k} (\mathbf{x}^{(i)}) \right|\right]\]We can intepret the sum of log determinants in the objective as each “layer” of the flow receiving additional gradient information about the objective.
While we discussed that \(f_\theta\) is a sequence of transformations, we didn’t cover how to define those transformations. Research in normalizing flow methods typically consists of constructing transformations that are easily invertible and have simple and computable log determinants. The most well-known normalizing flow methods are NICE, RealNVP and Glow. Many of these methods impose specific archictectural constraints on each neural network layer to ensure that it is invertible and that the Jacobian has some simple structure. For example, in the NICE paper, each transformation is a coupling layer that has a lower triangular Jacobian. The determinant of a triangular matrix is just the product of entries on the diagonal. The coupling layer transformation is quite simple. First we partition the input to layer \(K\) into two blocks \(\mathbf{x}_{K - 1} = [\mathbf{x}_{K - 1}^A, \mathbf{x}_{K - 1}^B]\). Then we compute the following:
\[\begin{align*} \mathbf{x}_{K}^A &= \mathbf{x}_{K - 1}^A \\ \mathbf{x}_{K}^B &= \mathbf{x}_{K - 1}^B + m_{\theta_K}(\mathbf{x}_{K - 1}^A), \end{align*}\]where \(m_\theta\) is some arbitrarly complex neural network at layer \(K\). Then \(\mathbf{x}_{K} = [\mathbf{x}_{K}^A, \mathbf{x}_{K}^B]\). In words, this transformation keeps the first block of the partition the same. The second block is updated/coupled with the first part based on some complicated function parameterized by a neural network. The inverse of this transformation can be obtain simply:
\[\begin{align*} \mathbf{x}_{K - 1}^A &= \mathbf{x}_{K}^A \\ \mathbf{x}_{K - 1}^B &= \mathbf{x}_{K}^B - m_{\theta_K}(\mathbf{x}_{K - 1}^A). \end{align*}\]The Jacobian of this transformation can be written as a lower triangular block matrix. We can see this by taking the derivative with respect to each part in the partitions. The following figure shows a visual depication of the transformation:
The next method we will cover is residual flows which will help us understand and motivate continuous normalizing flows.
Residual Flows
Many of the methods described above impose specific architectural constraints on the neural network to ensure that the transformation \(f_\theta\) is invertible. Furthermore, additional restrictions have to be placed in order to ensure the transformation has a sparse or structured Jacobian to make the log determinant easier to compute. Creating invertible neural network architectures with structured Jacobians is a difficult task that often leads to exotic designs, and in general, is a limiting approach to normalizing flows.
Residual flows make use of invertible-ResNets (i-ResNet) and compute an unbiased estimate of the log determinant. Unlike previous approaches there are no constraints on the Jacobian. These properties allow us to use more expressive architectures. In particular, there is a rather simple property that can be imposed on ResNets to make them invertible.
Recall that ResNets are a pretty simple architecture that consist of many residual blocks of the form:
\[\mathbf{x}_{t+1} = \mathbf{x_t} + g_{\theta_{t}}(\mathbf{x_t}).\]Simply transform the input \(\mathbf{x_t}\) via the neural network \(g_{\theta_{t}}\) at layer \(t\) and add it to itself. If we can find a way to make each layer invertible then the entire ResNet will be invertible. To understand how we can accomplish this, we first have to learn about the Banach fixed point theorem.
Suppose you have a contractive transformation \(T: \mathbb{R}^d \to \mathbb{R}^d\). Technically, \(T\) can map between any two general metric spaces but we will consider \(\mathbb{R}^d\) for simplicity. We say that the transformation \(T\) is contractive if there exists a constant \(K < 1\) such that for all \(\mathbf{x}, \mathbf{y} \in \mathbb{R}^d\),
\[\left\lVert T(\mathbf{x}) - T(\mathbf{y}) \right\rVert \leq K\left\lVert \mathbf{x} - \mathbf{y} \right\rVert.\]The Banach fixed point theorem states that there is a unique point \(\mathbf{x}\) such that \(T(\mathbf{x}) = \mathbf{x}\) i.e. \(\mathbf{x}\) is a fixed point that does not move under the transformation. In fact, we can compute \(\mathbf{x}\) using the following iterative procedure which provably converges. Select \(\mathbf{x}^{(0)} \in \mathbb{R}^d\) at random and then,
\[\mathbf{x}^{(n+1)} = T(\mathbf{x}^{(n)}).\]Intuitively, since \(T\) is contractive, the distances between images of the iterate \(\mathbf{x}^{(n)}\) and the fixed point \(\mathbf{x}\) under \(T\) will shrink. Since the distance is shrinking it must mean that the iterates are converging to the fixed point.
An equivalent way of stating that map \(T\) is contractive is declaring that \(T\) is \(L\)-Lipschitz continuous with constant \(L < 1\). To make a residual layer invertible, we are going to enforce that the neural network \(g_{\theta_t}\) is contractive i.e. it has \(L_t < 1\). Although this won’t provide us with an analytical form for the inverse, we can determine the inverse through an iterative routine. The proof of this is rather short. Suppose \(\mathbf{x}_{t+1} \in \mathbb{R}^d\) is arbitrary. We need to show that there exists a point \(\mathbf{x}_t\) such that \(\mathbf{x}_{t+1} = \mathbf{x}_t + g_{\theta_t}(\mathbf{x}_t)\). Let’s perform the following iterative routine with initial point \(\mathbf{y}^{(0)} = \mathbf{x}_{t+1}\):
\[\mathbf{y}^{(n+1)} = \mathbf{x}_{t+1} - g_{\theta_t}(\mathbf{y}^{(n)}).\]We are going to define transformation \(T_{\mathbf{x}_{t+1}}(\mathbf{w}) = \mathbf{x}_{t+1} - g_{\theta_t}(\mathbf{w})\). Notice that \(\mathbf{x}_{t+1}\) is a constant with respect to the transformation in \(\mathbf{w}\). Multiplying \(g_{\theta_t}\) by \(-1\) and adding a constant perserves the Lipschitz continuity and does not change the Lipschitz constant. Therefore, \(T_{\mathbf{x}_{t+1}}\) is also a contractive map. Therefore, there exists a point we will denote by \(\mathbf{x}_t\) that is a fixed point of the transformation and the above iterative routine is equivalent to the following:
\[\mathbf{y}^{(n+1)} = T_{\mathbf{x}_{t+1}}(\mathbf{y}^{(n)}).\]Therefore, the iterative subroutine will converge to fixed point \(\mathbf{x}_t\). Since \(\mathbf{x}_{t+1}\) was arbitrary and \(\mathbf{x_t}\) satisifies,
\[\mathbf{x}_t = \mathbf{x}_{t+1} - g_{\theta_t}(\mathbf{x}_t),\]the residual layer is invertible.
Now, how can we actually design a neural network \(g_{\theta_t}\) that will have a Lipschitz constant less than one? Fortunately, this does not require any complex architecture requirements. We can do this by using contractive activition functions such as \(\tanh\), ReLU and ELU and standard linear layers such as a feed-forward layer or convolutional layer. However, we must normalize the weight matrix of each layer, \(\mathbf{W}_i\) such that the spectral norm \(\left\lVert \mathbf{W}_i\right\rVert _2 \leq 1\). To do this, we compute an approximation of spectral norm of the unnormalized matrix and simply divide the unnormalized matrix by this approximation.
Once we have the invertible network, the next tricky part of residual flows is evaluating the log-determinant: \(\log\left\vert\det \frac{\partial f^{-1}_\theta}{\partial \mathbf{x}}\right\vert\) of the transformation. Interestingly, the log-determinant of each layer of the ResNet can be written as an infinite series of trace matrix powers:
\[\sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} \text{tr}\left[\left(\frac{\partial g_{\theta_t}}{\partial \mathbf{x}}\right)^k\right].\]We can compute an approximation of this infinite series by truncating it to the first \(N\) terms where \(N\) is a hyperparameter. The trace of the matrix in each term can be estimated using the Hutchinson trace estimator. The Hutchinson trace estimator computes an unbiased estimate of the trace using matrix vector products. Specifically, to compute the trace of matrix \(\mathbf{A}\), we need a random vector \(\mathbf{v}_i\) such that \(\mathbb{E}[\mathbf{v}^{}_i\mathbf{v}^\top _i] = \mathbf{I}\). Then,
\[\text{tr}[\mathbf{A}] = \frac{1}{V} \sum_{i=1}^{V} \mathbf{v}_i^\top \mathbf{A} \mathbf{v}_i.\]In practice, we only use one sample to estimate the trace. Although the trace estimation is unbiased, since we always truncate the original infinite series at \(N\) terms, the overall estimate will be biased.
To make the estimator unbiased, we need to introduce some randomness into the truncation and take an expectation. Fortunately, we can use the “Russian roulette” estimator. The formula for the estimator is quite involved so we present a high-level intuition. The basic idea is that we always evaluate the first term and to determine whether we should evaluate the remaining terms we flip a coin that has probability \(p\) of coming up heads. If the remaining terms are evaluated then they are reweighted by \(\frac{1}{p}\) which results in an unbiased estimate. Futhermore, the estimate has probability \(1 - p\) of being evaluated in finite time (the case where we only evaluate the first term). Interesingly, we can obtain an estimator that is evaluated in finite time with probability one. We simply have to apply this process infinitely many times to the terms that have yet to be computed. Eventually, we are gauranteed to flip a tail and stop computing. Also, just like before we use the Hutchinson trace estimator to estimate the trace of the matrix in each term. Thus, we can compute this infinite series as:
\[\mathbb{E}_{n, \mathbf{v}}\left[\sum_{k=1}^{n} \frac{(-1)^{k+1}}{\mathbb{P}(N \geq k)} \mathbf{v}^\top\left[\left(\frac{\partial g_{\theta_t}}{\partial \mathbf{x}}\right)^k\right]\mathbf{v}\right],\]where \(n \sim p(N)\) for some distribution \(p\) and \(\mathbf{v} \sim \mathcal{N}(0,1)\).
To summarize, we have introduced normalizing flows, a class of generative models that learn an invertible transformation between a noise distribution \(p\) and a data distribution \(q\). We briefly covered some normalizing flow methods such as NICE that impose specific architectural constraints to ensure an invertible neural network and computable Jacobian. We discussed residual flows in detail which avoid exotic architecture design by using invertible ResNets. Relatively simple design choices can ensure that ResNets are invertible. Then we discussed how to compute an unbiased estimator of the Jacobian in the case of residual flows. Overall, normalizing flows are a powerful framework for generative modeling. Their main drawbacks include the limitation regarding architecture design and the high computational cost of the determinant of the Jacobian. In the next blog post, we will attempt to address these issues with continuous normalizing flows.
Continuous Normalizing Flows
In the normalizing flows setup, the transformation from the simple distribution to the data distribution is expressed as a finite composition of functions. We can intepret this as a discrete time process with \(K\) time steps. At each time step, there is a corresponding intermediary distribution. But how can we obtain a transformation from \(p\) to \(q\) in continuous time rather than discrete time? Imagine this as taking the composition of infinitely many functions. We can express this idea using Ordinary Differential Equations (ODE), the fundamental component of Continuous Normalizing Flows (CNF).
There is an even deeper connection between ODEs and residual flows that will lead us to continuous time flows. We can write the residual layer more generally as,
\[\mathbf{x}_{t+1} = \mathbf{x}_t + h u(\mathbf{x}_t),\]where \(h > 0\) is some constant and \(u\) is the neural network. First, observe that this equation looks like the Euler discretization of an ODE. Following the analogy, \(\mathbf{x}_t\) represents the current point we are at. To get to the point \(\mathbf{x}_{t+1}\) we move in the direction of the derivative, \(u(\mathbf{x}_t)\) with step size \(h\). In fact, if we rearrange this equation, we start to see something that resembles the definition of the derivative,
\[\frac{\mathbf{x}_{t+1} - \mathbf{x}_t}{h} = u(\mathbf{x}_t).\]If we take \(h \to 0\) and increase the number of layers \(t \to \infty\) we arrive at the following ODE:
\[\frac{d\mathbf{x}(t)}{dt} = u_t(\mathbf{x}(t)),\]where \(u_t\) is a time varying vector field that we parameterize with a neural network with parameters \(\theta\). This is called a Neural Ordinary Differential Equation. When we first introduced residual flows, it may have seemed strange to denote the layers with a time parameter \(t\). Now we know that residual layers are just a discretization of the continuous time dynamics of an ODE. Also, since we have represented residual flows in continuous time, each layer does not have its own parameters. Instead, the parameters are shared across time. Now, we are modeling the time varying vector field that transforms a distribution \(p\) to \(q\). There are a few main benefits that we gain from using Neural ODEs.
1) The Euler discretization method is very rudimentary. ODEs and numerical integration is a mature field and we have much better numerical integrators at our disposal. With CNFs, we can use faster and more accurate solvers to integrate the time varying vector field we model with a neural network. Residual flows required specifying the number of layers of the ResNet which we no longer need to do. ODE solvers can determine the discretization steps needed to obtain a certain error threshold.
2) Discrete Normalizing flows required computing the determinant of the Jacobian matrix which is an \(\mathcal{O}(d^3)\) operation. As we will see, CNFs allow us to perform the same operation with some numerical approximation in just \(\mathcal{O}(d)\) time.
To gain some intuition for flows and ODEs, consider a two dimensional vector field \(v(x,y)\) that describes the movement of water flowing along a river. For simplicity, assume it’s time-independent. The velocity of the water at point \((x,y)\) is the vector \(v(x,y)\). The path of a pebble thrown into the water at time \(t=0\) is a curve we can parameterize as a function of time:
\[\mathbf{r}(t) = \langle x(t), y(t) \rangle, \qquad \mathbf{r}(0) = \langle x(0), y(0) \rangle.\]We can solve for the position of the pebble at time \(t\) by making the following observation. At time \(t\), the velocity of the pebble, \(\frac{d\mathbf{r}(t)}{dt}\), is the same as the velocity of the water at the position of the pebble, \(\mathbf{r}(t)\). We can model this with the following ODE:
\[\frac{d\mathbf{r}(t)}{dt} = v(\mathbf{r}(t)) = v(x(t), y(t)), \qquad \mathbf{r}(0) = \langle x(0), y(0) \rangle.\]This example demonstrate how we can describe the movement of a particle induced by a vector field given some initial position. Specifically, we can construct a function \(\mathbf{r}(t)\) that describes the path taken by a single particle starting at a specific point in space at \(t=0\). As we will see, a flow in the context of CNFs is a more general object that represents the motion of all particles through time.
Vector Field Examples
Let’s provide a more rigorous definition of a flow. Suppose we have a vector field \(u: \mathbb{R}^d \times [0, 1] \to \mathbb{R}^d\). Unlike the example above, this is a time-dependent vector field and we will denote the time parameter as a subscript, \(u_t(x)\). In this setup, \(d\) is the dimension of our data space.
A flow, which is induced by the vector field \(u_t\), is a mapping \(\phi: \mathbb{R}^d \times [0,1] \to \mathbb{R}^d\) which satisfies the following ODE:
\[\frac{d\phi_t(\mathbf{x})}{dt} = u_t(\phi_t(\mathbf{x})),\]with initial condition \(\phi_0(\mathbf{x}) = \mathbf{x}\).
To gain a better intiution of what \(\phi\) represents we can compare it to \(\mathbf{r}(t)\). Given some initial point \(\mathbf{x_0}\), \(\mathbf{r}(t)\) is the position of that point at time \(t\) induced by the movement of water. Similarly, when we provide \(\mathbf{x_0}\) as input to \(\phi\), we will get the function \(\phi(t, \mathbf{x_0}): [0, 1] \to \mathbb{R}^d\) which is only a function of time. It parameterizes a curve in \(\mathbb{R}^d\) that represents the position of the point \(\mathbf{x_0}\) with time induced by the vector field \(u_t\). We can view \(\phi\) from another perspective. Given a specific point in time \(t_0 \in [0,1]\) as input to \(\phi\), we will obtain a function \(\phi(t_0, \mathbf{x}): \mathbb{R}^d \to \mathbb{R}^d\). This function maps all points at time \(t=0\) to the position they would be at time \(t=t_0\). Overall, the mapping \(\phi\) describes the movement of all points starting from time \(t=0\) to time \(t = 1\).For consistent notation, we will denote the time parameter as a subscript \(\phi_t\).
Another important object in CNFs is the probability density path \({p_t: \mathbb{R}^d \times [0,1] \to \mathbb{R}_{>0}}\). It is a time-dependent probability density function i.e. \(\int p_t(\mathbf{x})d\mathbf{x} = 1\). Similar to normalizing flows, we let \(p_0 = p\) be a simple distribution such as a canonical Gaussian. Then \(p_t\) is defined by a change of variables from \(p_0\) using mapping \(\phi_t\):
\[\begin{equation}\label{COV_CNF} p_t(\mathbf{x}) = p_0(\phi_t^{-1}(\mathbf{x}))\det \left| \frac{\partial \phi_t^{-1}}{\partial \mathbf{x}}(\mathbf{x}) \right|. \end{equation}\]With some regularity conditions on \(u_t\), we can gaurauntee that \(\phi_t\) is invertible. Therefore, a vector field generates a single unique probability density path. This also implies that the paths generated by the flow ODE are non-crossing which can be shown by simple contradiction. Suppose the paths of two different points do overlap at some point in time \(t \in [0,1]\). This means that two different points are mapped to the same point at time \(t\). But this would mean that \(\phi_t\) is not an invertible mapping.
In the setting of CNFs, we let \(p_1\) be the data distibution. The goal is to learn a vector field \(v_t\) which induces a flow \(\phi_t\). This flow is responsible for transforming the simple distribution \(p_0 = p\) at time \(t=0\) to the data distribution \(p_1 = q\) at time \(t=1\).
The training objective is the same as in normalizing flows. We maximize the log-likelihood of the data. Given a data point \(\mathbf{x_1} \in \mathbb{R}^d\), to compute \(\log p_1(\mathbf{x_1})\) we could use Equation \(\eqref{COV_CNF}\). However, as in normalizing flows, that would require computing the Jacobian which is an \(O(d^3)\) operation. A benefit of CNFs is that once we are in the continuous setting, there is an alternative method available so we don’t have to do this computation. The alternative method involves the continuity equation:
\[\begin{equation}\label{cont_eq} \frac{\partial}{\partial t}p_t(\mathbf{x}) + \nabla \cdot (p_t(\mathbf{x})u_t(\mathbf{x})) = 0. \end{equation}\]The continuity equation is a Partial Differential Equation (PDE) where \(\nabla \cdot\) represents the divergence operator. The divergence is computed with respect to the spatial dimensions \(\frac{\partial}{\partial x_i}\). The continuity equation provides a necassary and sufficient condition to ensure that a vector field \(u_t\) generates the probability density path \(p_t\). A key detail to note is that a given probability density path can have infinitely many vector fields that generate it. Although, a specific vector field generates only one unique probability density path.
The continuity equation can be derived using some basic vector calculus. It also has a nice physics interpretation. Let’s start by considering an arbitary volume \(V\) in \(\mathbb{R}^3\) for the purposes of visualization. The volume \(V\) is enclosed by the surface \(S\). By definition, \(p_t\) has to integrate to \(1\) over \(\mathbb{R}^3\). This is a key observation. It means that analagous to mass, the probability density \(p_t\) is a conserved quantity. It cannot appear or disappear out of thin air. Therefore, the change in probability density across the volume must equal the difference in probablity density that has entered the volume and the density that has exited the volume. To gain some physical intiution, imagine \(u_t\) as the vector field representing the flow of water through the volume \(V\). Let \(p_t\) be the mass of the water. The change in mass of the flowing water in the volume must be the difference in the mass of water entering and mass of water leaving. So, we can write the change in probability density as follows:
\[\frac{d}{dt}\iiint_V p_t dV.\]The triple integral is the total mass or probability density inside the volume. To measure the change, we take the derivative. Notice the only way for density to enter or leave the volume is through the surface \(S\). Now, let \(n: \mathbb{R}^3 \to \mathbb{R}^3\) represent the outward normal vector to \(S\) at point \((x,y,z)\). Consider an infinitesimally small part of the surface \(S\). The flow of density entering or leaving is the dot product of the normal \(n\) in that small region and the flow vector field \(u_t\). Then the amount of probability density entering or leaving the small region is \((u_t \cdot n)p_t\). Therefore, the change of probability density can also be represented as
\[\frac{d}{dt}\iiint_V p_t dV = - \iint_S (u_t \cdot n) p_t dS.\]We have a negative sign because any density leaving the volume means a negative rate of change of the probability density. Now we can apply Gauss’s divergence theorem:
\[- \iint_S (u_t \cdot n) p_t dS = - \iiint_V \nabla \cdot (p_tu_t) dV.\]We have written the surface integral as a volume integral. Then,
\[\frac{d}{dt}\iiint_V p_t dV = - \iiint_V \nabla \cdot (p_tu_t) dV.\]Moving everything to one side and simplfying we get,
\[\iiint_V \left[ \frac{d}{dt}p_t + \nabla \cdot (p_tu_t) \right] dV = 0.\]Since this is true for any arbitrary volume \(V\) it must be that the quantity inside the integral is equal to \(0\). This results in the continuity equation.
Using the continuity equation and the ODE describing the flow \(\phi_t\) we get the instantaneous change of variable equation:
\[\frac{d}{dt}\log p_t(\phi_t(\mathbf{x})) + \nabla \cdot u_t(\phi_t(\mathbf{x})) = 0.\]The proof of this fact is rather short so we provide it here. Consider the total derivative of \(\log p_t(\phi_t(\mathbf{x}))\),
\[\begin{align} \frac{d\log p_t(\phi_t(\mathbf{x}))}{dt} &= \frac{\partial \log p_t(\phi_t(\mathbf{x}))}{\partial t} \cdot \frac{\partial t}{\partial t} + \nabla_{\mathbf{x}} \log p_t(\phi_t(\mathbf{x})) \cdot \frac{d \phi_t(\mathbf{x})}{d t} \notag \\ &= \frac{\partial \log p_t(\phi_t(\mathbf{x}))}{\partial t} + \nabla_{\mathbf{x}} \log p_t(\phi_t(\mathbf{x})) \cdot \frac{d \phi_t(\mathbf{x})}{d t} \notag \\ &= \frac{\partial \log p_t(\phi_t(\mathbf{x}))}{\partial t} + \nabla_{\mathbf{x}} \log p_t(\phi_t(\mathbf{x})) \cdot u_t(\phi_t(x)) \label{cov_deriv} \end{align}\]Notice the first term is the partial derivative with respect to \(t\). We can obtain this term by rearranging the continuity equation. One property of the divergence operator is that \(\nabla \cdot (p_t(\mathbf{x})u_t(\mathbf{x})) = p_t(\mathbf{x}) \nabla \cdot u_t(\mathbf{x}) + u_t(\mathbf{x}) \cdot \nabla_\mathbf{x} p_t(\mathbf{x})\). So the continuity equation becomes,
\[\begin{equation*} \frac{\partial}{\partial t}p_t(\phi_t(\mathbf{x})) + p_t(\phi_t(\mathbf{x})) \nabla \cdot u_t(\phi_t(\mathbf{x})) + u_t(\phi_t(\mathbf{x})) \cdot \nabla_\mathbf{x} p_t(\phi_t(\mathbf{x})) = 0. \end{equation*}\]Now divide by \(p_t(\phi_t(\mathbf{x}))\),
\[\begin{equation*} \frac{1}{p_t(\phi_t(\mathbf{x}))}\frac{\partial}{\partial t}p_t(\phi_t(\mathbf{x})) + \nabla \cdot u_t(\phi_t(\mathbf{x})) + u_t(\phi_t(\mathbf{x})) \cdot \nabla_\mathbf{x} \frac{p_t(\phi_t(\mathbf{x}))}{p_t(\phi_t(\mathbf{x}))} = 0. \end{equation*}\]Recognize the derivative of \(\log\) and move some terms to the other side to get,
\[\begin{equation*} \frac{\partial}{\partial t}\log p_t(\phi_t(\mathbf{x})) = -\nabla \cdot u_t(\phi_t(\mathbf{x})) - u_t(\phi_t(\mathbf{x})) \cdot \nabla_\mathbf{x} \log p_t(\phi_t(\mathbf{x})). \end{equation*}\]Now substitute this formula into \(\eqref{cov_deriv}\) to obtain the desired result. Remember that in the discrete normalizing flow setup, the change of variable formula required computing the determinant of the Jacobian which was a \(\mathcal{O}(d^3)\) operation. Using the instantaneous change of variables formula we can compute the log-likelihood by integrating the ODE,
\[\log p_1(\phi_1(\mathbf{x})) = \log p_0(\phi_0(\mathbf{x})) - \int_0^1 \nabla \cdot u_t(\phi_t(\mathbf{x})) dt.\]Observe that divergence with respect to the spatial dimension is the same as trace of the Jacobian of \(u_t\). Computing the trace is an \(\mathcal{O}(d^2)\) operation. Using Hutchinson’s trace estimator formula we can reduce the cost down to \(\mathcal{O}(d)\).
Now we have an ODE that describes the change of the log-probability along the flow trajectory. So how can we use this ODE to compute \(\log p_1(\mathbf{x_1})\), and train a CNF with maximum likelihood? So far, we have discussed ODEs in the forward direction i.e. increasing time which is needed to transform the noise distribution into a data distribution. We can also compute and solve ODEs in the reverse direction allowing us to transfrom \(q\) to \(p\). In order to compute the log-likelihood of the data, we need to use the reverse direction ODE. First, we sample a point \(\mathbf{x_1}\) from \(q\). Then we solve the reverse ODE,
\[\frac{d\phi_{1-s}(\mathbf{x})}{ds} = -u_{1-s}(\phi_{1-s}(\mathbf{x})),\]with initial condition \(\phi_1(\mathbf{x}) = \mathbf{x_1}\) with \(s \in [0,1]\). The solution to this is a point \(\mathbf{x_0}\) from the noise distribution. Now we can solve the reverse ODE corresponding to instantenous change of variables formula,
\[\frac{d}{ds}\log p_{1-s}(\phi_{1-s}(\mathbf{x})) = \nabla \cdot u_{1-s}(\phi_{1-s}(\mathbf{x})).\]with initial condition \(\log p_0(\phi_0(\mathbf{x})) = \log p(\mathbf{x_0})\). The fact that \(p_0 = p\) is a simple distribution is a key property because that allows us to evaluate the log-likelihood \(\log p_0(\mathbf{x_0})\). Instead of having to evaluate the \(u_{1-s}\) again to solve this ODE, we can solve the log-likelihood and flow trajectory in a coupled manner:
\[\frac{d}{ds} \begin{bmatrix} \phi_{1-s}(\mathbf{x}) \\ f(1-s) \end{bmatrix} = \begin{bmatrix} -u_{1-s}(\phi_{1-s}(\mathbf{x})) \\ \nabla \cdot u_{1-s}(\phi_{1-s}(\mathbf{x})) \end{bmatrix}\]with \(f(t) = \log p_t(\phi_t(\mathbf{x})) - \log p_1(\phi_1(\mathbf{x}))\). At \(t=1\) we want the difference between the two likelihoods to match so our initial condition is \(f(1) = 0\). The combined initial conditions are,
\[\begin{bmatrix} \phi_{1}(\mathbf{x}) \\ f(1) \end{bmatrix} = \begin{bmatrix} \mathbf{x_1} \\ 0 \end{bmatrix}.\]To summarize, we can train CNFs with maximum likelihood using reverse ODEs. Unlike training discrete normalizing flows which require computing the determinant with cost \(\mathcal{O}(d^3)\), CNFs only need \(\mathcal{O}(d)\) for computing the divergence. However, there is still a downside to training CNFs. The caveat is we have to simulate the flow trajectory to obtain the log-probability. Simulation is very slow even with the \(\mathcal{O}(d)\) operation cost. As a result, continuous normalizing flows scale very poorly which is why they were not as popular as other deep generative methods. In the next blog post, we will discuss flow matching which aims to solve this issue.
Flow Matching
Flow Matching (FM) builds on the same framework as CNFs but uses a different loss function. The main motivation to use this loss function is to address the scalability issue with the maximum likelihood computation. Furthermore, we will see that flow matching will allow for arbitrary source distributions \(p\) and we will not be restricted to simple noise distributions such as the standard Gaussian.
To motivate the FM loss, consider the continuity equation. It provides a direct correspondence between the probability density path \(p_t\) and the vector field \(u_t\). Namely, if we knew the vector field already, then we know it generates a unique probability density path. Therefore, instead of directly optimizing the probability density path and having to compute \(\log p_1(\mathbf{x_1})\), we can optimize the vector field instead. Assuming that we know the probability density path and its generating vector field, the flow matching loss is defined as follows:
\[\mathcal{L}_{FM}(\theta) = \mathbb{E}_{t,p_t(\mathbf{x})}\left\lVert v_t(\mathbf{x}) - u_t(\mathbf{x})\right\rVert^2,\]where \(v_t(x)\) is a learnable vector field parameterized by \(\theta\). We let \(p_t\) be the probability density path where \(p_0 = p\) is a simple source distribution and \(p_1\) is the data distribution \(q\). We regress the learnable vector field \(v_t\) onto the true vector field, \(u_t\). The FM loss is somewhat comparable to score-based generative modelling where we learn the score function (which can be seen as a time-independent vector field) in a regressive manner. Intuitively, we take an expectation over time \(t \in [0,1]\) because we are interested in learning a time dependent vector field. We take an expectation over the probability density path given time \(t\) since we want to regress the vector field onto points that are likely under the probability path it generates. This would be more effecient at learning an accurate vector field than randomly sampling points in \(\mathbb{R}^d\) under some arbitrary distribution.
Although the FM loss seems to solve the problem with CNFs, the major caveat of course, is in practice, we cannot compute this loss because we don’t know \(p_t\) or \(u_t\). If we did then obviously there would be no point in learning the vector field \(v_t\). To overcome this obstacle, we are going to create another loss that will be computable. This is the conditional flow matching loss:
\[\begin{equation}\label{CFM_loss} \mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t,q(\mathbf{x_1}), p_t(\mathbf{x}\vert\mathbf{x_1})}\left\lVert v_t(\mathbf{x}) - u_t(\mathbf{x}\vert\mathbf{x_1})\right\rVert^2. \end{equation}\]We can prove that \(\nabla_\theta \mathcal{L}_{FM}\) and \(\nabla_\theta \mathcal{L}_{CFM}\) are equal upto a constant. So they are equivalent in a sense since they have the same optima. This makes the conditional flow matching loss a reasonable replacement. Now, we will describe conditional flow matching (CFM) and the objects in the conditional flow matching loss.
The basic idea is that we can construct the marginal probability path by “averaging” conditional probability paths. These conditional paths are conditioned on data samples. Suppose we have a particular sample \(\mathbf{x_1}\) from the data distribution. We design the conditional probability path, \(p_t(\mathbf{x} \vert \mathbf{x_1})\) to satisfy the following boundary conditions: \(p_0(\mathbf{x}\vert\mathbf{x_1}) = p\) and \(p_1(\mathbf{x} \vert \mathbf{x_1}) = q\). Then we can marginalize over the data distribution to obtain the marginal probability density path,
\[p_t(\mathbf{x}) = \int p_t(\mathbf{x}|\mathbf{x_1})q(\mathbf{x_1})d\mathbf{x_1}.\]From this, we can see that constructing the conditional probability path so \(p_0(\mathbf{x} \vert\mathbf{x_1}) = p_0(\mathbf{x})\) and \(p_1(\mathbf{x} \vert\mathbf{x_1}) = \delta_{\mathbf{x_1}}\) results in \(p_0(\mathbf{x}) = p(\mathbf{x})\) and \(p_1(\mathbf{x}) = q(\mathbf{x})\).
For a given conditional probability path, there exists a conditional vector field which generates the path. The conditional vector field is denoted as \(u_t(x\vert\mathbf{x_1})\). Interestingly, we can compute the marginal vector field by also marginalizing over the data distribution in the following manner,
\[\begin{align*} u_t(\mathbf{x}) = \int u_t(\mathbf{x} \vert \mathbf{x_1})\frac{p_t(\mathbf{x} \vert \mathbf{x_1})q(\mathbf{x_1})}{p_t(\mathbf{x})}d\mathbf{x_1}. \end{align*}\]The key realization is that the marginal vector field constructed above actually generates the marginal probability path. We can prove this by showing that \(u_t\) and \(p_t\) satisfy the continuity equation but the calculations are left out for brevity. Since \(p_0 = p\) and \(p_1 = q\), we have a method of transporting the source distribution to the data distribution just by using simple conditional probability paths. Furthermore, we can also define the conditional flow, \(\phi_t(\mathbf{x}\vert \mathbf{x_1})\) which satisfies the following ODE based on the conditional vector field:
\[\begin{equation}\label{CFM_ODE} \frac{d}{dt}\phi_t(\mathbf{x} \vert \mathbf{x_1}) = u_t\left(\phi_t(\mathbf{x} \vert \mathbf{x_1}) \vert \mathbf{x_1}\right), \end{equation}\]with initial condition \(\phi_0(\mathbf{x} \vert \mathbf{x_1}) = \mathbf{x}\). The conditional flow generates the probability density path through the change of variables equation. Also, as before, we can integrate over the conditional vector field to obtain the conditional flow.
So, if we have a way of defining the marginal vector field and probability density path which transforms \(p\) to \(q\), why do we have to use the conditional flow matching loss? This is because computing the integral over conditional vector fields is still intractable. Thus, we need a loss function that does not require computing \(u_t\).
Returning back to the conditional flow matching loss, the main idea is that we take an expectation over the data distribution and the conditional probability path. As a result, we can replace the marginal vector field in the flow matching loss with the conditional vector field. In practice, we sample a point from the dataset and then sample from the conditional probability path instead of the marginal probability path. Of course, computing the loss also involves sampling a time \(t \in [0,1]\).
Furthermore, we can make the following observation to reparameterize the conditional flow matching loss. The reparameterization avoids having to sample \(\mathbf{x} \sim p_t(\mathbf{x} \vert \mathbf{x_1})\). Instead, we can sample \(\mathbf{x_0} \sim p\) from the simple distribution. Then \(\mathbf{x_t} = \phi_t(\mathbf{x_0} \vert \mathbf{x_1})\) is a sample from \(p_t(\mathbf{x} \vert \mathbf{x_1})\) since the conditional flow is a transformation from \(p\) to \(p_t(\mathbf{x} \vert \mathbf{x_1})\). Therefore, \(\mathbf{x_t}\) is the solution to the ODE in Equation \(\eqref{CFM_ODE}\) with \(\mathbf{x_0}\) substituted into the flow:
\[\frac{d\phi_t(\mathbf{x_0}|\mathbf{x_1})}{dt} = \mu_t(\phi_t(\mathbf{x_0}|\mathbf{x_1}) \vert \mathbf{x_1}),\]with initial condition \(\phi_0(\mathbf{x_0}\vert\mathbf{x_1}) = \mathbf{x_0}\). Therefore, we can rewrite the conditional flow matching objective as:
\[\begin{align} \mathcal{L}_{CFM}(\theta) &= \mathbb{E}_{t, q(\mathbf{x_1}), p(\mathbf{x_0})}\left\lVert v_t(\phi_t(\mathbf{x_0}|\mathbf{x_1})) - \mu_t(\phi_t(\mathbf{x_0}|\mathbf{x_1}) | \mathbf{x_1})\right\rVert^2 \notag \\ &= \mathbb{E}_{t, q(\mathbf{x_1}), p(\mathbf{x_0})}\left\lVert v_t(\phi_t(\mathbf{x_0}|\mathbf{x_1})) - \frac{d\phi_t(\mathbf{x_0}|\mathbf{x_1})}{dt}\right\rVert^2. \label{reparam_CFM_loss} \end{align}\]To summarize, we have a way of training CNFs by using conditional probability paths and flows. The conditional flow matching loss has the same optima and doesn’t require access to the marginal probability path or vector field. We can compute the conditional flow matching loss effeciently as long as \(p_t(\mathbf{x}\vert\mathbf{x_1})\) is defined and can be sampled from effeciently. Furthermore, we are able to easily compute \(u_t(\mathbf{x}\vert\mathbf{x_1})\) because it is defined on a per-sample basis.
Flow matching does not require simulating the flow or solving an ODE during training unlike training CNFs with the maximum likelihood objective. This makes training CNFs with flow matching more stable and effecient. In order to generate new samples, first sample \(\mathbf{x_0} \sim p\) from the noise distribution and then use a solver to find the solution, \(\phi_1(\mathbf{x_0})\) to the flow matching ODE with the learned vector field:
\[\frac{d\phi_t(\mathbf{x_0})}{dt} = v_t(\phi_t(\mathbf{x_0})),\]with initial condition \(\phi_0(\mathbf{x_0}) = \mathbf{x_0}\).
We have covered the basics of the conditional flow matching framework but have not specified the conditional probability path or conditional flow. These aspects are design choices and it is up to us to choose how we define \(p_t(\mathbf{x} \vert \mathbf{x_1})\) and \(\phi_t(\mathbf{x} \vert \mathbf{x_1})\). Broadly speaking, there are two ways we can make these choices:
-
Probability path perspective. Notice that the conditional flow matching objective in Equation \(\eqref{CFM_loss}\) just requires defining the conditional probability path \(p(\mathbf{x} \vert \mathbf{x_1})\) that satisfies the boundary conditions. Once a conditional probability path is defined, we can obtain the conditional vector field by solving the continuity equation \(\eqref{cont_eq}\). However, solving for \(u_t(\mathbf{x} \vert \mathbf{x_1})\) is usually very difficult. Also, in this case, the flow is defined implicity since once we have a vector field we can solve the conditional flow matching ODE in Equation \(\eqref{CFM_ODE}\) to get the flow.
-
Interpolant perspective. The reparameterized flow matching loss in Equation \(\eqref{reparam_CFM_loss}\) requires defining the prior distribution \(p\) and the conditional flow \(\phi_t(\mathbf{x} \vert \mathbf{x_1})\). In this case, the conditional probability path is defined implicity and we can obtain it by applying \(\phi_t(\mathbf{x} \vert \mathbf{x_1})\) to the prior \(p\) using the change of variables formula. Also, we could solve for \(p_t(\mathbf{x} \vert \mathbf{x_1})\) using the continuity equation but that would be harder. But notice that we don’t need \(p_t(\mathbf{x} \vert \mathbf{x_1})\) to train the reparameterized objective and we also don’t need it for sampling because we use the learned vector field \(v_t\). As a result, the interpolant perspective is usually the easier approach.
To define these objects, we will follow the approach taken by the original flow matching paper by (cite). The definitions for these objects are motivated primarily by simplicity and tractability. Due to the simplicity of their approach, we will see that it can be viewed both from the probability path and interpolant perspective. Flow matching was introduced as a vector field \(u_t\) inducing a flow \(\phi_t\) that results in a probability density path \(p_t\). Although this is the natural way to understand the framework, we are going to define these objects in the opposite order but everything still works out.
We start off by defining the conditional probability path. As a reminder, the simple source distribution \(p\) will be a canonical Gaussian. Therefore, to satisfy the first boundary condition, we must have \(p_0(\mathbf{x}\vert\mathbf{x_1}) = \mathcal{N}(\mathbf{0}, \mathbf{I})\). The second boundary condition is \(p_1(\mathbf{x} \vert\mathbf{x_1}) = \delta_{\mathbf{x_1}}\). For numerical reasons, we approximate the Dirac-delta distribution with a small variance Gaussian \(\mathcal{N}(\mathbf{x_1}, \sigma^2_{min}\mathbf{I})\). Given the boundary conditions, a natural and simple choice for the conditional probability path is a Gaussian distribution for each time \(t\),
\[p_t(\mathbf{x}\vert\mathbf{x_1}) = \mathcal{N}(u_t(\mathbf{x_1}), \sigma^2_t(\mathbf{x_1})\mathbf{I}),\]where \(u_t: \mathbb{R}^d \times [0,1] \to \mathbb{R}^d\) and \(\sigma: \mathbb{R}^d \times [0,1] \to \mathbb{R}_{>0}\) are the time-dependent mean and standard deviation. In order to satisfy the boundary conditions, we must have that \(u_0(\mathbf{x_1}) = 0\), \(\sigma_0(\mathbf{x_1}) = 1\), \(u_1(\mathbf{x_1}) = \mathbf{x_1}\) and \(\sigma_1(\mathbf{x_1}) = \sigma_{min}\).
The simplest conditional flow that will generate \(p_t(\mathbf{x} \vert \mathbf{x_1})\) given that \(p\) is a canonical Gaussian is the following:
\[\phi_t(\mathbf{x} \vert\mathbf{x_1}) = \sigma_t(\mathbf{x_1})\mathbf{x} + u_t(\mathbf{x_1}),\]where \(\mathbf{x} \sim p\). Indeed by example 1, this is true.
The conditional vector field that generates this flow is given by the following:
\[u_t(\mathbf{x}\vert\mathbf{x_1}) = \frac{\sigma_t'(\mathbf{x_1})}{\sigma_t(\mathbf{x_1})}(\mathbf{x} - \mu_t(\mathbf{x_1})) + \mu'_t(\mathbf{x_1}).\]In this setup, \(\mu_t\) is an arbitrary function that we can choose. Essentially, this allows us to select any arbitrary path from \(0\) to \(\mathbf{x_1}\). A natural choice for this is a straight line which is called the optimal transport solution.
Optimal Transport
The optimal transport solution is the path that requires the least amount of work done to transform the canonical Gaussian to the mean \(u_t\) and std. \(\sigma_t\) Gaussian. Specifically, the mean and standard deviation change linearly with time:
\[u_t(\mathbf{x}) = t\mathbf{x_1}, \quad \text{and} \quad \sigma_t(\mathbf{x}) = 1 - (1 - \sigma_{min})t.\]This straight line path is generated by the vector field:
\[u_t(\mathbf{x} \vert \mathbf{x_1}) = \frac{\mathbf{x_1} - (1 - \sigma_{min})\mathbf{x}}{1 - (1 - \sigma_{min})t}.\]By substituting \(u_t\) and \(\sigma_t\), we get that the conditional flow in optimal transport case is:
\[\phi_t(\mathbf{x}|\mathbf{x_1}) = [1- (1 - \sigma_{min})t]\mathbf{x} + t\mathbf{x_1}.\]Therefore, the reparameterized conditional flow matching loss is the following,
\[\mathbb{E}_{t, q(\mathbf{x_1}), p(\mathbf{x_0})}\left\lVert v_t(\phi_t(\mathbf{x_0}|\mathbf{x_1})) - (\mathbf{x_1} - (1 - \sigma_{min})\mathbf{x_0})\right\rVert^2.\]The conditional flow is the optimal transport displacement map between two Gaussians. Although, the conditional flow is optimal it doesn’t imply that the marginal vector field is the optimal transport map between \(p\) and \(q\).
To summarize, in this section, we covered the conditional flow matching framework using Gaussian probability paths with a canonical Gaussian source distribution. In this particular case, the probability path is simple enough that we can define the conditional flow and vector field using the probability path perspective or the interpolant perspective. Furthermore, the conditional flow matching framework is not restricted to Gaussian probability paths. We can have a different source distribution and use a different conditional path given that it satisifies the boundary conditions. However, designing probability paths for arbitrary source distributions may be difficult.
iCFM and OT-CFM
In the previous section, we covered the conditional flow matching framework that was introduced by Lipman et al. (2023). There are two main limitations of the approach that they proposed. In this section, we introduce independent Conditional Flow Matching (iCFM) and Optimal Transport Conditional Flow Matching (OT-CFM) that will address these two limitations. In order to do this, we are going to reformulate CFM in a slightly more general form and then we will see that iCFM and OT-CFM are particular instantiations of this general CFM.
The first limitation we want to address is finding a way to work with a source distribution that has an intractible probability density function. This can be done by conditioning on the source distribution in addition to the target/data distribution. To generalize, we condition on some variable \(\mathbf{z}\) that is distributed according to some distribution \(\tilde{q}\). In the conditional flow matching loss, we use to the conditional probability path, \(p_t(\mathbf{x} \vert \mathbf{z})\) and condition vector field \(u_t(\mathbf{x} \vert \mathbf{z})\):
\[\mathcal{L}(\theta) = \mathbb{E}_{t, \tilde{q}(\mathbf{z}), p_t(\mathbf{x} \vert \mathbf{z})} \lVert v_t(\mathbf{x}) - u_t(\mathbf{x} \vert \mathbf{z}) \rVert.\]The work by Lipman et al. (2023) conditions on the target distribution so \(\tilde{q} = q\) and \(\mathbf{z} = \mathbf{x_1}\). In the iCFM framework, we let \(\mathbf{z} = (\mathbf{x_0}, \mathbf{x_1})\) where \(\tilde{q}(\mathbf{z}) = p(\mathbf{x_0})q(\mathbf{x_1})\). So \(\mathbf{z}\) represents a point from the source distribution and data distribution which are sampled independently from each other. The conditional flow transports a Gaussian with a small variance centered at \(\mathbf{x_0}\) to a Gaussian with small variance centered at \(\mathbf{x_1}\). The conditional probability path and conditional vector field are:
\[p_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1}) = \mathcal{N}((1-t)\mathbf{x_0} + t\mathbf{x_1}, \sigma_{min}), \qquad u_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1}) = \mathbf{x_1} - \mathbf{x_0}.\]Also, the conditional flow generated by this vector field is the following:
\[\begin{align*} \phi_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1}) &= \mathbf{x} - \mathbf{x_0} + (1-t)\mathbf{x_0} + t\mathbf{x_1} \\ &= t(\mathbf{x_1} - \mathbf{x_0}) + \mathbf{x}. \end{align*}\]In order to obtain the marginal probability path \(p_t\), we must marginalize with respect to \(\mathbf{z}\) which is \(\mathbf{x_1}, \mathbf{x_0}\) in this case:
\[p_t(\mathbf{x}) = \int_{\mathbf{x_1}} \int_{\mathbf{x_0}} p_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1}) p(\mathbf{x_0}) q(\mathbf{x_1}) d\mathbf{x_0}d\mathbf{x_1}.\]At \(t=0\), we have that \(p_0(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1}) = \mathcal{N}(\mathbf{x_0}, \sigma_{min})\) which does not dependent on \(\mathbf{x_1}\). Therefore,
\[p_0 = \int_{\mathbf{x_0}} p_0(\mathbf{x} \vert \mathbf{x_0}) p(\mathbf{x_0}) d\mathbf{x_0}.\]As \(\sigma_{min} \to 0\), the conditional path at \(t=0\) becomes a dirac-delta distribution centered at \(\mathbf{x_1}\). In that case the marginal path at \(t=0\) corresponds exactly to the source distribution \(p\). Of course, we use a Gaussian with small variance to approximate the dirac delta distribution so the marginal probability path at \(t=0\) is \(p_0 = p \star \mathcal{N}(\mathbf{0}, \sigma_{min}^2\mathbf{I})\) where \(\star\) is the convolutional operator. Using similar reasoning, the marginal probability path at \(t=1\) is \(p_1 = q \star \mathcal{N}(\mathbf{0}, \sigma_{min}^2\mathbf{I})\). Therefore, the conditional probability path and vector field transport \(p_0\) to \(p_1\) which are approximately \(p\) and \(q\). If we use dirac-delta distributions instead, we would transport \(p\) to \(q\) exactly.
This also highlights a difference between CFM and iCFM. In CFM, the conditional probability path at \(t=0\) must be the same as the source distribution \(p\). However, in iCFM the conditional path at \(t=0\) does not correspond to the source distribution. Furthermore, since iCFM conditions the probability path on the source distribution, we do not need a source distribution that has a tractible probability density. We just need to be able to sample from the source distribution. This is the added flexibility that flow matching provides. Diffusion models can only learn how to transform a noise distribution (e.g. Gaussian) to a data distribution. With flow matching, we can go from any source to target distribution. This allows us to use more informative source distributions rather than just a complete noisy distribution such as a Gaussian. For example, if we want to generate molecules, we might already have another dataset of similar molecules which we can use as a source distribution.
One of the issues of CFM that iCFM fails to address is the fact that the marginal vector field is not the optimal transport solution from \(p\) to \(q\). Recall that there are potentially infinitely many vector fields that transform distribution \(p\) to \(q\). Just because the conditional vector fields of CFM and iCFM are optimal, it doesn’t imply that the marginal vector field is. But what does it mean for a vector field to be the optimal transport solution?
The solution to the static optimal transport problem minimizes the distance between two probability measures based on some cost function \(c(\mathbf{x},\mathbf{y})\). The 2-Wasserstein distance corresponds to using the L2 norm, \(c(\mathbf{x},\mathbf{y}) = \lVert \mathbf{x} - \mathbf{y} \rVert _2^2\). Then the \(2\)-Wasserstein distance between distributions \(p\) and \(q\), \(W_2^2(p,q)\) is defined as the solution to the following optimization problem,
\[W_2^2(p,q) = \min_{\pi \in \Gamma(p,q)} \mathbb{E}_{\pi(\mathbf{x_0}, \mathbf{x_1})} \left[\lVert \mathbf{x_0} - \mathbf{x_1} \rVert _2^2\right],\]where \(\Gamma(p,q)\) denotes the set of probability measures on \(\mathbb{R}^d \times \mathbb{R}^d\) with left marginal \(p\) and right marginal \(q\). We denote the minimizer as \(\pi^\star\) and it is also called the optimal coupling. Intuitively, the optimization problem captures the cost of transforming distribution \(p\) to distribution \(q\). One of the interesting aspects of the \(2\)-Wasserstein distance is that we can reformulate the optimization problem in terms of vectors fields \(u_t\) that generate probability density paths \(p_t\),
\[W_2^2(p,q) = \min_{u_t, p_t} \int_0^1 \int_{\mathbb{R}^d} p_t(\mathbf{x}) \lVert u_t(\mathbf{x}) \rVert _2^2 d\mathbf{x}dt,\]where \(p_0 = p\) and \(p_1 = q\) (i.e. \(p_t\) satisifies the boundary conditions). This is called the dynamic formulation of the optimal transport problem and is equivalent to the static formulation. But why would we be interested in obtaining a vector field \(u_t\) that is a solution to the optimal transport problem? In the static formulation, we want to minimize the distance between the start and end points. In the dynamic formulation, we can see a term that takes into account the norm of the vector field. Intuitively, we are encouraging the lengths of the path taken by the flow to be as short as possible. Thus, the paths generated by the optimal vector field will be straight lines. This is helpful because straight line paths are easy to simulate during inference and they reduce the variance of the gradient objective during training which helps optimization.
In fact, we can empirically observe non-straight flow paths generated by the marginal vector field learned through the CFM and iCFM framework. In the figure below, we have two mixtures of Gaussians represented with the source distribution in purple and target distribution in red. The image one the right shows simulated flow paths of the learned marginal vector field. The most logical paths generated by the marginal vector field should transport points from the top purple mixture to the top red mixture and the bottom purple mixture to the bottom red mixture. However, during training the source and target data points are sampled independently, so there are conditional flow paths \(\phi_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1})\) that mix top and bottom mixtures. As a result, the learned marginal vector field produces curved marginal flow paths. This means that a lot of points are being pushed towards the curved part and the marginal vector field is changing rapidly during the curved part. This behaviour makes integrating across the vector field more numerically unstable so simulating the flow during inference becomes slow because we would have to use smaller step sizes in the ODE solver.
Furthermore, we can see that the conditional flow paths cross each other. Of course this happens because we sample pairs that contain one point from a top mixture and the other point from a bottom mixture. The problem with this is that during training, we are regressing the learnable marginal vector field onto the conditional vector fields whose corresponding paths cross each other. However, the marginal vector field cannot generate paths that cross each other. This inconsistency results in the loss function having a large variance of gradient estimates during training which slows down optimization. Also, note that the conditional flow paths arising from the same conditional vector field do not intersect by uniqueness of the ODE. The problem arises because conditional flow paths from different vector fields can interstect i.e. paths from \(u_t(\mathbf{x} \vert \mathbf{x_0}, \mathbf{x_1})\) and \(u_t(\mathbf{x} \vert \tilde{\mathbf{x_0}}, \tilde{\mathbf{x_1})}\) can intersect.

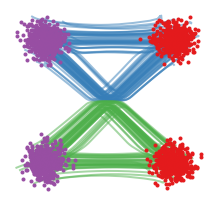
To quickly summarize, the main issues with CFM and iCFM is that the marginal vector field is not gauranteed to have straight paths leading to slow inference and the conditional flows can cross each other leading to slow training speed. The reason for this is that iCFM samples points \(\mathbf{z} = (\mathbf{x_0}, \mathbf{x_1})\) independently i.e. \(\tilde{q}(\mathbf{z}) = p(\mathbf{x_0})q(\mathbf{x_1})\). OT-CFM resolves these problems by using the o
In order to resolve this problem, we will choose a different distribution \(\tilde{q}\) for \(\mathbf{z}\) which will result in the OT-CFM method. Instead of sampling \(\mathbf{x_0}\) and \(\mathbf{x_1}\) independently as in \(\tilde{q}(\mathbf{z}) = p(\mathbf{x_0})q(\mathbf{x_1})\) we define \(\tilde{q}\) to be the \(2\)-Wasserstein optimal transport map \(\pi\),
\[\tilde{q}(\mathbf{z}) \pi(\mathbf{x_0}, \mathbf{x_1}).\]Riemannian Flow Matching (RFM)
In the previous section, we discussed how to do flow matching in \(\mathbb{R}^d\). Another interesting question is how do we do flow matching on non-Euclidean geometries? This is relevant if you already know that your data lies on a manifold.
Figure 2: Consider a simple case where your data lies on a simple manifold in \(\mathbb{R}^2\) - the circle. Of course, on the left-hand side, you can use flow matching on Euclidean spaces to try to model this data. But it may be beneficial to specify as much prior knowledge you have about the data to obtain the best model. So performing flow matching on the manifold domain, the circle represented on the right, may lead to better performance.
There are many real-world applications where we would want to model data that resides on a manifold. Examples include protein modelling, molecule modelling, robotics, medical imaging and geological sciences.
In this section, we introduce Riemannian flow matching - a generalization of flow matching. Specifically, we consider complete, connected and smooth Riemannian manifolds, \(\mathcal{M}\) endowed with metric \(g\). Formally, we have a set of data samples \(\{x_i\}_{i=1}^N\) with \(x_i \in \mathcal{M}\) that arise from a probability distribution, \(q\) on \(\mathcal{M}\). We aim to learn a flow that transforms a simple noise distribution \(p\) on \(\mathcal{M}\) to the data distribution.
The tangent space at \(x \in \mathcal{M}\) is denoted as \(T_x\mathcal{M}\). Also, \(g\) induces many key quantities. It defines an inner product over \(T_x\mathcal{M}\) denoted as \(\langle u,v \rangle _g\). We have the expontential map \(\exp_x: T_x\mathcal{M} \to \mathcal{M}\) and extensions of the gradient, divergence and Laplacian. For all \(x \in \mathcal{M}\), \(\text{div}_g{x}\) denotes the divergence with respect to the spatial (\(x\)) argument. The integration of the function \(f: \mathcal{M} \to \mathbb{R}\) is denotes as \(\int f(x) d\text{vol}_x\).
Fortunately, there is not too many changes required to make flow matching work on manifolds. The objects used in RFM are the same as in FM. The space of probability densities over \(\mathcal{M}\) is defined as \(\mathcal{P}\). We have a probability path \(p_t: \mathcal{M} \times [0,1] \to \mathcal{P}\) such that \(\int p_t(x)d\text{vol}_x = 1\). The time dependent vector field is represented as \(u_t: \mathcal{M} \times [0,1] \to \mathcal{M}\). The flow \(\phi_t: \mathcal{M} \times [0,1] \to \mathcal{M}\) satisifies the following ODE defined on \(\mathcal{M}\):
\[\frac{d\phi_t(\mathbf{x})}{dt} = u_t(\phi_t(\mathbf{x})),\]with initial condition \(\phi_0(\mathbf{x}) = \mathbf{x}\). The vector field \(u_t\) and probability path \(p_t\) also satisify the continuity equation on manifolds:
\[\frac{dp_t(\mathbf{x})}{dt} + \text{div}_g u_t(\phi_t(\mathbf{x})) = 0.\]The vector field \(u_t\) generates the probability path \(p_t\) such that \(p_0 = p\) is the simple distribution and \(p_1 = q\) is the data distribution. The Riemannian flow matching objective is almost the same except we use \(g\) as the metric for the norm:
\[\mathcal{L}_{RFM}(\theta) = \mathbb{E}_{t, p_t(\mathbf{x})} \left\lVert v_t(\mathbf{x}) - u_t(\mathbf{x})\right\rVert^2_g.\]Again, \(v_t\) is a learnable time-dependent vector field parameterized by \(\theta\). However, as before we don’t know the probability path \(p_t\) nor the vector field that generates this probability path. Since we cannot compute this loss, we use the Riemannian conditional flow matching loss instead.
We condition on data samples to construct the conditional probability path and conditional vector field. Given \(\mathbf{x_1} \sim q\) we define the conditional path as \(p_t(\mathbf{x}\vert\mathbf{x_1})\) to satisfy the boundary conditions. As a note, we are keeping it general and not specifying the form of the conditional distribution. It does not have to be a Gaussian as in the Euclidean flow matching. Also, we can write the marginal probability path as
\[p_t(\mathbf{x}) = \int_{\mathcal{M}} p_t(\mathbf{x}\vert\mathbf{x_1})q(\mathbf{x_1})d\text{vol}_{\mathbf{x_1}}.\]We define the conditional vector field \(u_t(\mathbf{x}\vert\mathbf{x_1})\) that generates this probability path. The marginal vector field can be obtained in a similar fashion as before:
\[u_t(x) = \int_{\mathcal{M}} u_t(x|\mathbf{x_1}) \frac{p_t(x|\mathbf{x_1})q(\mathbf{x_1})}{p_t(x)} d\text{vol}_{\mathbf{x_1}}.\]Once again computing this integral is intractable which motivates us to define the Riemannian conditional flow matching loss:
\[\mathcal{L}_{RCFM}(\theta) = \mathbb{E}_{t, q(\mathbf{x_1}), p_t(\mathbf{x}\vert\mathbf{x_1})} ||v_t(\mathbf{x}) - u_t(\mathbf{x}\vert\mathbf{x_1})||^2_g.\]We can reparameterize the loss as follows:
\[\mathcal{L}_{RCFM}(\theta) = \mathbb{E}_{t, q(\mathbf{x_1}), r(\mathbf{x_0})} \left\lVert v_t(\phi_t(\mathbf{x}\vert\mathbf{x_0})) - u_t(\phi(\mathbf{x} \vert \mathbf{x_0})\vert\mathbf{x_1})\right\rVert^2_g.\]Now we need a way to construct the conditional flow. The conditional flow will map all points to \(\mathbf{x_1}\) at time \(t=1\) regardless of the choice of \(p\). So the flow satisfies:
\[\phi_1(\mathbf{x}\vert\mathbf{x_1}) = \mathbf{x_1}, \quad \forall \mathbf{x} \in \mathcal{M}.\]Also, in the same manner in which we parameterized the loss function, we can sample \(\mathbf{x_0} \sim p\) and then compute \(\mathbf{x_t} = \phi_t(\mathbf{x_0} \vert \mathbf{x_1})\). Now, in order to construct the conditional flow, we consider two different cases. The first case is when we are on simple manifolds i.e. we have a closed form for the geodesics. Let \(d_g(\mathbf{x}, \mathbf{y})\) represent the geodesic distance between two points on the manifold. Let \(\kappa(t)\) be a monotonically decreasing function s.t. \(\kappa(0) = 1\) and \(\kappa(1) = 0\). We want to find a conditional flow \(\phi_t(\mathbf{x} \vert \mathbf{x_1})\) that will satisfy the following equation according to the scheduler \(\kappa\):
\[d_g(\phi_t(\mathbf{x_0} \vert \mathbf{x_1}), \mathbf{x_1}) = \kappa(t)d_g(\mathbf{x_0}, \mathbf{x_1}).\]This will gaurantee that \(\phi_1(\mathbf{x} \vert \mathbf{x_1}) = \mathbf{x_1}\). A simple choice for this scheduler is \(\kappa(t) = 1 - t\). In fact, the conditional flow, \(\phi_t(\mathbf{x_0} \vert \mathbf{x_1})\) is a geodesic connecting \(x_0\) and \(x_1\). Additionally, the geodesic can be expressed as,
\[\phi_t(\mathbf{x_0} \vert \mathbf{x_1}) = \exp_{\mathbf{x_1}}(\kappa(t)\log_{\mathbf{x_1}}(\mathbf{x_0})),\]which is simple to compute and results in a highly-scalable training objective. This conditional flow can be thought of as the analouge of interpolating between \(\mathbf{x_0}\) and \(\mathbf{x_1}\) in Euclidean space:
\[(1 - \kappa(t))\mathbf{x_1} + \kappa(t)\mathbf{x_0}.\]When we are not on simple manifolds and don’t have access to the geodesic in closed form, we have to work with a pre-metric. A pre-metric is a function \(d: \mathcal{M} \times \mathcal{M} \to \mathbb{R}\) which satisfies the following properties:
- Non-negative: \(d(\mathbf{x}, \mathbf{y}) \geq 0\) for all \(x, y \in \mathcal{M}\)
- Positive: \(d(\mathbf{x}, \mathbf{y}) = 0\) iff \(x = y\)
- Non-degenerate: \(\nabla_x d(\mathbf{x}, \mathbf{y}) \neq 0\) iff \(x \neq y\)
Note that a geodesic satisfies the definition for a premetric. Then we want a flow \(\phi_t(\mathbf{x_0} \vert \mathbf{x_1})\) to satisfy,
\[d(\phi_t(\mathbf{x_0} \vert \mathbf{x_1}), \mathbf{x_1}) = \kappa(t)d(\mathbf{x_0}, \mathbf{x_1}).\]Once again, this will gaurantee that \(\phi_1(\mathbf{x_0} \vert \mathbf{x_1}) = \mathbf{x_1}\). Furthermore, the conditional vector field that generates this flow can be shown to be:
\[\mu_t(\mathbf{x} \vert \mathbf{x_1}) = \frac{d \log \kappa(t)}{dt} d(\mathbf{x}, \mathbf{x_1})\frac{\nabla_x d(\mathbf{x}, \mathbf{x_1})}{\lVert \nabla_x d(\mathbf{x}, \mathbf{x_1}) \rVert _g^2}.\]Although this formula seems complicated, the basic component is the gradient of the distance, \(\nabla_x d(\mathbf{x}, \mathbf{x_1})\). This ensures we are going in the direction of \(\mathbf{x_1}\). The other terms control for the speed and make sure that the flow hits \(\mathbf{x_1}\) at time \(t=1\).
If we don’t have access to the geodesic then there is no simple closed form interpolation like formula to compute \(\mathbf{x_t}\). Therefore, we must simulate/use an ODE solver to obtain \(\mathbf{x_t}\) which may computationally expensive.
An example of a pre-metric is the spectral distance:
\[d_w(\mathbf{x},\mathbf{y})^2 = \sum_{i=1}^{\infty} w(\lambda_i) (\varphi_i(\mathbf{x}) - \varphi_i(\mathbf{y})),\]where \(\varphi_i: \mathcal{M} \to \mathbb{R}\) are the eigenfunctions of the Laplace-Beltrami operator \(\Delta_g\) over \(\mathcal{M}\) with eigenvalues \(\lambda_i\), \(\Delta_g \varphi_i = \lambda_i \varphi_i\) and \(w: \mathbb{R} \to \mathbb{R}_{>0}\) is some monotonically decreasing weighting function. Using the spectral distance can be more beneficial than geodesics because they are more robust to topological noise such as holes and shortcuts and are more geometry aware. An example of a spectral distance is the biharmonic distance which is helpful in avoiding boundaries of manifolds as show in the following figure.