A Unified Framework for Diffusion Distillation

The explosive growth in one-step and few-step diffusion models has taken the field deep into the weeds of complex notations. In this blog, we cut through the confusion by proposing a coherent set of notations that reveal the connections among these methods.

Introduction

Diffusion and flow-based models have taken over the generative AI space, enabling unprecedented capabilities in videos, audios, and text generation. Nonetheless, there is a caveat⚠️ — they are painfully slow during inference. Generating a single high-quality sample requires running through hundreds of denoising steps, which translate to high costs and long wait times.

At its core, diffusion models (equivalently, flow matching models) operate by iteratively refining noisy data into high-quality outputs through a series of denoising steps. Similar to divide-and-conquer algorithms Common ones like Mergesort, locating the median and Fast Fourier Transform., diffusion models first divide the difficult denoising task into subtasks and conquer one of these at a time during training. To obtain a sample, we make a sequence of recursive predictions which means we need to conquer the entire task end-to-end.

This challenge has spurred research into acceleration strategies across multiple granular levels, including hardware optimization, mixed precision training, quantization, parameter-efficient fine-tuning, and advanced solver. In this blog, we focus on an orthogonal approach named Ordinary Differential Equation (ODE) distillation. This method introduces an auxiliary structure that bypasses explicit ODE solving, thereby reducing the Number of Function Evaluations (NFEs). As a result, we can generate high-quality samples with fewer denoising steps.

Distillation, in general, is a technique that transfers knowledge from a complex, high-performance model (the teacher) to a more efficient, customized model (the student). Recent distillation methods have achieved remarkable reductions in sampling steps, from hundreds to a few and even one step, while preserving the sample quality. This advancement paves the way for real-time applications and deployment in resource-constrained environments.

A video illustrating the basic flow matching concepts and three categories of ODE distillation objectives.

Notation at a Glance

The modern approaches of generative modelling consist of picking some samples from a base distribution \(\mathbf{x}_{1} \sim p_{\text{noise}}\), typically an isotropic Gaussian, and learning a map such that \(\mathbf{x}_{0} \sim p_{\text{data}}\). The connection between these two distributions can be expressed by establishing an initial value problem controlled by the velocity field \(v(\mathbf{x}_{t}, t)\),

\[\require{physics} \begin{equation} \dv{\psi_t(\mathbf{x}_t)}{t}=v(\psi_t(\mathbf{x}_t), t),\quad\psi_0(\mathbf{x}_0)=\mathbf{x}_0,\quad \mathbf{x}_0\sim p_{\text{data}} \label{eq:1} \end{equation}\]

where the flow \(\psi_t:\mathbb{R}^d\times[0,1]\to \mathbb{R}^d\) is a diffeomorphic map with \(\psi_t(\mathbf{x}_t)\) defined as the solution to the above ODE (\ref{eq:1}). If the flow satisfies the push-forward equationThis is also known as the change of variable equation: $[\phi_t]_\# p_0(x) = p_0(\phi_t^{-1}(x)) \det \left[ \frac{\partial \phi_t^{-1}}{\partial x}(x) \right].$ \(p_t=[\psi_t]_\#p_0\), we say a probability path \((p_t)_{t\in[0,1]}\) is generated from the velocity vector field. The goal of flow matching is to find a velocity field \(v_\theta(\mathbf{x}_t, t)\) so that it transforms \(\mathbf{x}_1\sim p_{\text{noise}}\) to \(\mathbf{x}_0\sim p_{\text{data}}\) when integrated. In order to receive supervision at each time step, one must predefine a condition probability path \(p_t(\cdot \vert \mathbf{x}_0)\)In practice, the most common one is the Gaussian conditional probability path. This arises from a Gaussian conditional vector field, whose analytical form can be derived from the continuity equation. $$\frac{\partial p_t}{\partial t} + \nabla \cdot (p_t v) = 0$$ See the table for details. associated with its velocity field. For each datapoint \(\mathbf{x}_0\in \mathbb{R}^d\), let \(v(\mathbf{x}_t, t\vert\mathbf{x}_0)=\mathbb{E}_{p_t(v_t \vert \mathbf{x}_0)}[v_t]\) denote a conditional velocity vector field so that the corresponding ODE (\ref{eq:1}) yields the conditional flow.

From left to right:conditional and marginal probability paths, conditional and marginal velocity fields. The velocity field induces a flow that dictates its instantaneous movement across all points in space.

Most of the conditional probability paths are designed as the differentiable interpolation between noise and data for simplicity, and we can express sampling from a marginal path \(\mathbf{x}_t = \alpha(t)\mathbf{x}_0 + \beta(t)\mathbf{x}_1\) where \(\alpha(t), \beta(t)\) are predefined schedules. The stochastic interpolant paper defines this probability path that summarizes all diffusion models, with several assumptions. Here, we use a simpler interpolant for clean illustration.

We provide some popular instances We ignore the diffusion models with SDE formulation like DDPM or ScoreSDE on purpose since we concentrate on ODE distillation in this blog. of these schedules in the table below.

Method Probability Path \(p_t\) Vector Field \(u(\mathbf{x}_t, t\vert\mathbf{x}_0)\)
Gaussian \(\mathcal{N}(\alpha(t)\mathbf{x}_0,\beta^2(t)I_d)\) \(\left(\dot{\alpha}_t - \frac{\dot{\beta}_t}{\beta_t}\alpha_t\right) \mathbf{x}_0 + \frac{\dot{\beta}_t}{\beta_t}\mathbf{x}_1\)
FM \(\mathcal{N}(t\mathbf{x}_1, (1-t+\sigma t)^2I_d)\) \(\frac{\mathbf{x}_1 - (1-\sigma)\mathbf{x}_t}{1-\sigma+\sigma t}\)
iCFM \(\mathcal{N}( t\mathbf{x}_1 + (1-t)\mathbf{x}_0, \sigma^2I_d)\) \(\mathbf{x}_1 - \mathbf{x}_0\)
OT-CFM Same prob. path above with \(q(z) = \pi(\mathbf{x}_0, \mathbf{x}_1)\) \(\mathbf{x}_1 - \mathbf{x}_0\)
VP-SI \(\mathcal{N}( \cos(\pi t/2)\mathbf{x}_0 + \sin(\pi t/2)\mathbf{x}_1, \sigma^2I_d)\) \(\frac{\pi}{2}(\cos(\pi t/2)\mathbf{x}_1 - \sin(\pi t/2)\mathbf{x}_0)\)

The simplest form of conditional probability path is \(\mathbf{x}_t = (1-t)\mathbf{x}_0 + t\mathbf{x}_1\) with the corresponding default conditional velocity field OT target \(v(\mathbf{x}_t, t \vert \mathbf{x}_0)=\mathbb{E}[\dot{\mathbf{x}}_t\vert \mathbf{x}_0]=\mathbf{x}_1- \mathbf{x}_0.\)

Borrowed from this slide at ICML2025, the objectives of ODE distillation have been categorized into three cases, i.e., (a) forward loss, (b) backward loss and (c) self-consistency loss.

Training: Since minimizing the conditional Flow Matching (FM) loss is equivalent to minimize the marginal FM loss, the optimization problem becomes

\[\arg\min_\theta\mathbb{E}_{\mathbf{x}_0, \mathbf{x}_1, t} \left[ w(t) \left\| v_\theta(\mathbf{x}_t, t) - v(\mathbf{x}_t, t | \mathbf{x}_0) \right\|_2^2 \right]\]

where \(w(t)\) is a reweighting functionThe weighting function modulates the contribution of the loss at each time step. This is necessary because the nature of the task differs fundamentally between high and low noise levels, requiring a balanced treatment of the loss across these regimes. Some common ones are included in this blog https://diffusionflow.github.io/..

Sampling: Solve the ODE \(\require{physics} \dv{\mathbf{x}_t}{t}=v_\theta(\mathbf{x}_t, t)\) from the initial condition \(\mathbf{x}_1\sim p_{\text{noise}}.\) Typically, an Euler solver or another high-order ODE solver is employed, taking a few hundred discrete steps through iterative refinements.

ODE Distillation methods

Before introducing ODE distillation methods, it is imperative to define a general continuous-time flow map \(f_{t\to s}(\mathbf{x}_t, t, s)\) where it maps any noisy input \(\mathbf{x}_t, t\in[0,1]\) to any point \(\mathbf{x}_s, s\in[0,1]\) on the ODE (\ref{eq:1}) that describes the probability flow aformentioned. This is a generalization of flow-based distillation and consistency models within a single unified framework. The flow map is well-defined only if its boundary conditions satisfy \(f_{t\to t}(\mathbf{x}_t, t, t) = \mathbf{x}_t\) for all time steps. One popular way to meet the condition is to parameterize the model as \(f_{t\to s}(\mathbf{x}_t, t, s)= c_{\text{skip}}(t, s)\mathbf{x}_t + c_{\text{out}}(t,s)F_{t\to s}(\mathbf{x}_t, t, s)\) where \(c_{\text{skip}}(t, t) = 1\) and \(c_{\text{out}}(t, t) = 0\) for all \(t\).

At its core, ODE distillation boils down to how to strategically construct the training objective of the flow map \(f_{t\to s}(\mathbf{x}_t, t, s)\) so that it can be efficiently evaluated during sampling. In addition, we need to orchestrate the schedule of \((t,s)\) pairs for better training dynamics.

In the context of distillation, the forward direction \(s<t\) is typically taken as the target. Yet, the other direction can also carry meaningful structure. Notice in DDIM sampling, the conditional probability path is traversed twice. In our flow map formulation, this can be replaced with the flow maps \(f_{\tau_i\to 0}(\mathbf{x}_{\tau_i}, \tau_i, 0), f_{0\to \tau_{i-1}}(\mathbf{x}_0, 0, \tau_{i-1})\) where \(0<\tau_{i-1}<\tau_i<1\). Intuitively, the flow map \(f_{t\to s}(\mathbf{x}_t, t, s)\) represents a direct mapping of some displacement field where \(F_{t\to s}(\mathbf{x}_t, t, s)\) measures the increment which corresponds to a velocity field.

MeanFlow

MeanFlow can be trained from scratch or distilled from a pretrained FM model. The conditional probability path is defined as the linear interpolation between noise and data \(\mathbf{x}_t = (1-t)\mathbf{x}_0 + t\mathbf{x}_1\) with the corresponding default conditional velocity field OT target \(v(\mathbf{x}_t, t \vert \mathbf{x}_0)=\mathbf{x}_1- \mathbf{x}_0.\) The main contribution consists of identifying and defining an average velocity field which coincides with our flow map as

\[F_{t\to s}(\mathbf{x}_t, t, s)=u(\mathbf{x}_t, t, s) \triangleq \frac{1}{t - s} \int_s^t v(\mathbf{x}_\tau, \tau) d\tau=\dfrac{f_{t\to s}(\mathbf{x}_t, t, s)-f_{t\to t}(\mathbf{x}_t, t, t)}{s-t}\]

where \(c_{\text{out}}(t,s)=s-t\). This is great since it attributes actual physical meaning to our flow map. In particular, \(f_{t\to s}(\mathbf{x}_t, t, s)\) represents the “displacement” from \(\mathbf{x}_t\) to \(\mathbf{x}_s\), while \(F_{t\to s}(\mathbf{x}_t, t, s)\) is the average velocity field pointing from \(\mathbf{x}_t\) to \(\mathbf{x}_s\).

We rearrange equation above.

\[\begin{equation} (t-s)F_{t\to s}(\mathbf{x}_t, t, s)=\int_s^t v(\mathbf{x}_\tau, \tau) d\tau \label{eq:2} \end{equation}\]

Differentiating (\ref{eq:2}) both sides w.r.t. $t$ and considering the assumption that $s$ is independent of $t$, we obtain the MeanFlow identity

\[\require{physics} v(\mathbf{x}_t, t)=F_{t\to s}(\mathbf{x}_t, t, s) +(t-s)\dv{F_{t\to s}(\mathbf{x}_t, t, s)}{t}\]

where we further compute the total derivative and derive the target \(F_{t\to s}^{\text{tgt}}(\mathbf{x}_t, t, s)\).

Training: Adapting to our flow map notation, the training objective turns to

\[\mathbb{E}_{\mathbf{x}_0, \mathbf{x}_1, t, s} \left[ w(t) \left\| F^\theta_{t\to s}(\mathbf{x}_t, t, s) - F_{t\to s}^{\text{tgt}}(\mathbf{x}_t, t, s | \mathbf{x}_0) \right\|_2^2 \right]\]

where \(F_{t\to s}^{\text{tgt}}(\mathbf{x}_t, t, s\vert\mathbf{x}_0)=v - (t-s)(v\partial_{\mathbf{x}_t}F^{\theta^-}_{t\to s}(\mathbf{x}_t, t, s) + \partial_t F^{\theta^-}_{t\to s}(\mathbf{x}_t, t, s))\) and \(\theta^-\) means stopgrad(). Note stopgrad aims to avoid high order gradient computation. There are a couple of choices for \(v\), we can substitute it with \(F_{t\to t}(\mathbf{x}_t, t, t)\) or \(v(\mathbf{x}_t, t \vert \mathbf{x}_0)=\mathbf{x}_1- \mathbf{x}_0.\) Again, MeanFlow adopts the latter to reduce computation.

Full derivation of the target Based on the MeanFlow identity, we can compute the target as follows: $$ \require{physics} \begin{align*} F_{t\to s}^{\text{tgt}}(\mathbf{x}_t, t, s\vert\mathbf{x}_0) &= \dv{\mathbf{x}_t}{t} - (t-s)\dv{F_{t\to s}(\mathbf{x}_t, t, s)}{t} \\ & = \dv{\mathbf{x}_t}{t} - (t-s)\left(\nabla_{\mathbf{x}_t} F_{t\to s}(\mathbf{x}_t, t, s) \dv{\mathbf{x}_t}{t} + \partial_t F_{t\to s}(\mathbf{x}_t, t, s) + \underbrace{\partial_s F_{t\to s}(\mathbf{x}_t, t, s) \dv{s}{t}}_{=0}\right) \\ & = v - (t-s)\left(v \nabla_{\mathbf{x}_t} F_{t\to s}(\mathbf{x}_t, t, s) + \partial_t F_{t\to s}(\mathbf{x}_t, t, s)\right). \\ \end{align*} $$ Note that in MeanFlow $$\require{physics}\dv{\mathbf{x}_t}{t} = v(\mathbf{x}_t, t\vert \mathbf{x}_0)$$ and $$\require{physics}\dv{s}{t}=0$$ since $s$ is independent of $t$.

In practice, the total derivative of \(F_{t\to s}(\mathbf{x}_t, t, s)\) and the evaluation can be done in a single function call: f, dfdt=jvp(f_theta, (xt, s, t), (v, 0, 1)). Despite jvp operation only introduces one extra backward pass, it still incurs instability and slows down training. Moreover, the jvp operation is currently incompatible with the latest attention architecture. SplitMeanFlow circumvents this issue by enforcing another consistency identity \((t-s)F_{t\to s} = (t-r)F_{t\to r}+(r-s)F_{r\to s}\) where \(s<r<t\). This implies a discretized version of the MeanFlow objective which falls into loss type (c).

Loss type Type (b) backward loss

Sampling: Either one-step or multi-step sampling can be performed. It is intuitive to obtain the following expression by the definition of average velocity field

\[\mathbf{x}_s = \mathbf{x}_t - (t-s)F^\theta_{t\to s}(\mathbf{x}_t, t, s).\]

In particular, we achieve one-step inference by setting $t=1, s=0$ and sampling from \(\mathbf{x}_1\sim p_{\text{noise}}\).

Consistency Models

Essentially, consistency models (CMs) are our flow map when \(s=0\), i.e., \(f_{t\to 0}(\mathbf{x}_t, t, 0).\)

Discretized CM

CMs are trained to have consistent outputs between adjacent timesteps along the ODE (\ref{eq:1}) trajectory. They can be trained from scratch by consistency training or distilled from given diffusion or flow models via consistency distillation like MeanFlow.

\[\mathbb{E}_{\mathbf{x}_t, t} \left[ w(t) d\left(f_{t \to 0}^\theta(\mathbf{x}_t, t,0), f_{t \to 0}^{\theta^-}(\mathbf{x}_{t-\Delta t}, t - \Delta t,0)\right) \right],\]

where \(\theta^-\) denotes \(\text{stopgrad}(\theta)\), \(w(t)\) is a weighting function, \(\Delta t > 0\) is the distance between adjacent time steps, and $d(\cdot, \cdot)$ is a distance metric.Common choices include $\ell_2$ loss $d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||_2^2$, pseudo-Huber loss $d(\mathbf{x}, \mathbf{y}) = \sqrt{||\mathbf{x} - \mathbf{y}||_2^2 + c^2} - c$ and Learned Perceptual Image Patch Similarity (LPIPS) loss.

\[\hat{\mathbf{x}}_0 = f^{\theta}_{1\to 0}(\mathbf{x}_1, 1,0),\]

while multi-step sampling is also possible since we can compute the next noisy output \(\mathbf{x}_{t-\Delta t}\sim p_{t-\Delta t}(\cdot\vert \mathbf{x}_0)\) using the prescribed conditional probability path at our discretion. Discrete-time CMs depend heavily on the choice of \(\Delta t\) and often require carefully designed annealing schedules. To obtain the noisy sample \(\mathbf{x}_{t-\Delta t}\) at the previous step, one typically evolves backward \(\mathbf{x}_t\) by numerically solving the ODE (\ref{eq:1}), which can introduce additional discretization errors.

Continuous CM

When using \(d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||_2^2\) and taking the limit $\Delta t \to 0$, Song et al. show that the gradient of the discretized CM’s loss with respect to $\theta$ converges to a new objective with no \(\Delta t\) involved.

\[\require{physics} \mathbb{E}_{\mathbf{x}_t, t} \left[ w(t) (f^\theta_{t\to 0})^{\top}(\mathbf{x}_t, t,0) \dv{f^{\theta^-}_{t\to 0}(\mathbf{x}_t, t,0)}{t} \right]\]

where \(\require{physics} \dv{f^{\theta^-}_{t\to 0}(\mathbf{x}_t, t,0)}{t} = \nabla_{\mathbf{x}_t} f^{\theta^-}_{t\to 0}(\mathbf{x}_t, t,0) \dv{\mathbf{x}_t}{t} + \partial_t f^{\theta^-}_{t\to 0}(\mathbf{x}_t, t,0)\) is the tangent of \(f^{\theta^-}_{t\to 0}\) at \((\mathbf{x}_t, t)\) along the trajectory of the ODE (\ref{eq:1}). Consistency Trajectory Models (CTMs) extend this objective so that the forward loss (type (a)) becomes globally optimized. In this context, their intuition is that \(f^\theta_{t \to s}(\mathbf{x}_t, t, s)\approx f^\theta_{r \to s}(\texttt{Solver}_{t\to r}(\mathbf{x}_t, t, r), r, s).\) The composition order on the right-hand side depends on the assumption of the solver of the teacher model.

Same as the Discretized Version. CTMs introduce a new sampling method called \(\gamma\)-sampling which controls the noise level of diffusing the intermediate noisy sample according to the conditional probability path during multi-step sampling.

Loss type Type (b) backward loss, while CTMs optimize type (a) forward loss, both locally and globally.

Flow Anchor Consistency Model

Similar to MeanFlow preliminaries, Flow Anchor Consistency Model (FACM) also adopts the linear conditional probability path \(\mathbf{x}_t = (1-t)\mathbf{x}_0 + t\mathbf{x}_1\) with the corresponding default conditional velocity field OT target \(v(\mathbf{x}_t, t \vert \mathbf{x}_0)=\mathbf{x}_1- \mathbf{x}_0.\) In our flow maps notation, FACM parameterizes the model as \(f^\theta_{t\to s}(\mathbf{x}_t, t, 0)= \mathbf{x}_t - tF^\theta_{t\to s}(\mathbf{x}_t, t, 0)\) where \(c_{\text{skip}}(t,s)=1\) and \(c_{\text{out}}(t,s)=-t\).

FACM imposes a consistency property which requires the total derivative of the consistency function to be zero

\[\require{physics} \dv{t}f^\theta_{t \to 0}(\mathbf{x}, t, 0) = 0.\]

This is intuitive since every point on the same probability flow ODE (\ref{eq:1}) trajectory should be mapped to the same clean data point \(\mathbf{x}_0\).

By substituting the parameterization of FACM, we have

\[\require{physics} F^\theta_{t\to 0}(\mathbf{x}_t, t, 0)=v(\mathbf{x}_t, t)-t\dv{F^\theta_{t\to 0}(\mathbf{x}_t, t, 0)}{t}.\]

Notice this is equivalent to MeanFlow where \(s=0\). This indicates CM objective directly forces the network \(F^\theta_{t\to 0}(\mathbf{x}_t, t, 0)\) to learn the properties of an average velocity field heading towards the data distribution, thus enabling the 1-step generation shortcut.

Training: FACM training algorithm equipped with our flow map notation. Notice that \(d_1, d_2\) are $\ell_2$ with cosine loss$L_{\cos}(\mathbf{x}, \mathbf{y}) = 1 - \dfrac{\mathbf{x} \cdot \mathbf{y}}{\|\mathbf{x}\|_{2} \, \|\mathbf{y}\|_{2}}$ and norm $\ell_2$ loss$L_{\text{norm}}(\mathbf{x}, \mathbf{y}) =\dfrac{\|\mathbf{x}-\mathbf{y}\|^2}{\sqrt{\|\mathbf{x}-\mathbf{y}\|^2+c}}$ where $c$ is a small constant. This is a special case of adaptive L2 loss proposed in MeanFlow. respectively, plus reweighting. Interestingly, they separate the training of FM and CM on disentangled time intervals. When training with CM target, we let \(s=0, t\in[0,1]\). On the other hand, we set \(t'=2-t, t'\in[1,2]\) when training with FM anchors.

The modified training algorithm of FACM. All the notations are adapted to our flow map.

Sampling: Same as CM.

Loss type Type (b) backward loss

Align Your Flow

Our notation incorporates a small modification of the flow map introduced by Align Your Flow, where we indicate the direction of the distillation. Hence, we say that Align Your Flow (AYF) the continuous-time flow map \(f^{\text{AYF}}(\mathbf{x}_t, t, s)=f_{t\to s}(\mathbf{x}_t, t, s).\) Specifically, AYF selects a tighter set of boundary conditions \(c_{\text{skip}}(t,s)=1\) and \(c_{\text{out}}(t,s)=s-t\).

Training: The first variant of the objective, called AYF-Eulerian Map Distillation, is compatible with both distillation and training from scratch.

\[\nabla_\theta \mathbb{E}_{\mathbf{x}_t, t, s}\left[w(t, s)\text{sign}(t - s) \cdot (f^\theta_{t \to s})^\top(\mathbf{x}_t, t, s) \cdot \frac{\text{d}f^{\theta^-}_{t\to s}(\mathbf{x}_t, t, s)}{\text{d}t}\right]\]

It is intriguing that this objective reduces to the continuous CM objective when \(s=0\), while transforming to original FM objective when \(s\to t\)The gradient of AYF-EMD matches the gradient of FM objective up to some constant when taking the limit $s\to t$.. In addition, CTMs uses a discrete consistency loss with a fixed discretized time schedule comparing to AYF-EMD objective. Regarding the second variant, named AYF-Lagrangian Map Distillation, it is only applicable to distillation from a pretrained flow model \(F^\delta_{t \to t}(\mathbf{x}_t,t,t)\).

\[\nabla_\theta \mathbb{E}_{\mathbf{x}_t, t, s}\left[w(t, s)\text{sign}(s - t) \cdot (f^\theta_{t \to s})^\top \cdot \left(\frac{\text{d}f^{\theta^-}_{t\to s}}{\text{d}s} - F^\delta_{s \to s}((f_{\theta^-}(\mathbf{x}_t, t, s), s,s)\right)\right].\]

Sampling: Same as CM. A combination of \(\gamma\)-sampling and classifier-free guidance.

The formulation of these objectives is majorly built on the Flow Map Matching. Similar to the trick in training Meanflow and CMs, they add a stopgrad operator to the loss to stabilize training and make the objective practical. In their appendix, they provide a detailed proof of why these objectives are equivalent to the objectives in Flow Map Matching.

Loss type Type (b) backward loss for AYF-EMD, type (a) forward loss for AYF-LMD.

Connections

Now it is time to connect the dots with some previous existing methods. Let’s frame their objectives in our flow map notation and identify their loss types if possible.

Shortcut Models

The diagram of Shortcut Models

In essence, Shortcut Models augment the standard flow matching objective with a self-consistency regularization term. This additional loss component ensures that the learned vector field satisfies a midpoint consistency property: the result of a single large integration step should match the composition of two smaller steps traversing the same portion of the ODE (\ref{eq:1}) trajectory.

Training: In the training objective, we neglect the input arguments and focus on the core transition between time steps. Again, we elaborate it with our flow map notation.

\[\mathbb{E}_{\mathbf{x}_t, t, s}\left[\left\|F^\theta_{t\to t} - \dfrac{\text{d}\mathbf{x}_t}{\text{d}t}\right\|_2^2 + \left\|f^\theta_{t\to s} - f^{\theta^-}_{\frac{t+s}{2}\to s}\circ f^{\theta^-}_{t \to \frac{t+s}{2}}\right\|_2^2\right]\]

where we adopt the same flow map conditions based on AYF.

Sampling: Same with MeanFlow yet with specific shortcut lengths.

Loss type Type (c) tri-consistency loss

ReFlow

The diagram of rectified flow and ReFlow process

Unlike most ODE distillation methods that learn to jump from \(t\to s\) according to our defined flow map \(f_{t\to s}(\mathbf{x}_t, t, s)\), ReFlow takes a different approach by establishing new noise-data couplings so that the new model will generate straighter trajectories.In the rectified flow paper, the straightness of any continuously differentiable process $$Z=\{Z_t\}$$ can be measured by $$S(Z)=\int_0^1\mathbb{E}\|(Z_1-Z_0)-\dot{Z}_t\|^2 dt$$ where $S(Z)=0$ implies the trajectories are perfectly straight. In this case, this allows the ODE (\ref{eq:1}) to be solved with fewer steps and larger step sizes. To some extent, this resembles the preconditioning from OT-CFM where they intentionally sample noise and data pairs jointly from an optimal transport map \(\pi(\mathbf{x}_0, \mathbf{x}_1)\) instead of independent marginals.

Training: Pair synthesized data from the pretrained model with the noise. Use this new coupling to train a student model with the standard FM objective.

Sampling: Same as FMs.

Inductive Moment Matching

The diagram of IMM

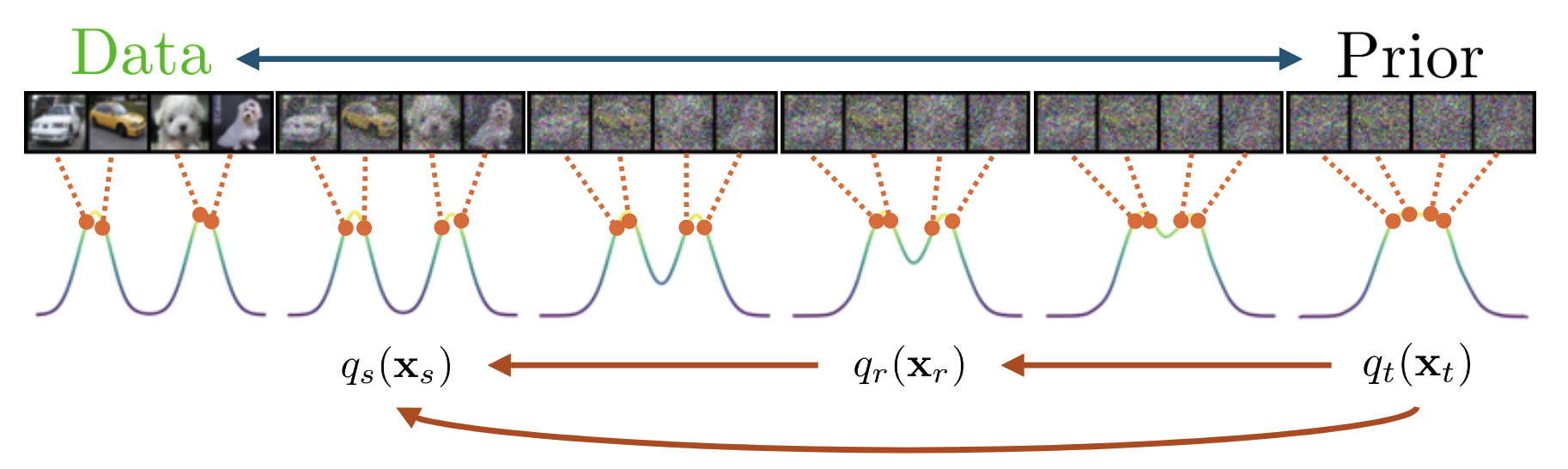
This recent method trains our flow map from scratch via matching the distributions of \(f^{\theta}_{t\to s}(\mathbf{x}_t, t, s)\) and \(f^{\theta}_{r\to s}(\mathbf{x}_r, r, s)\) where \(s<r<t\). They adopt an Maximum Mean Discrepancy (MMD) loss to match the distributions.

Training: In our flow map notation, the training objective becomes

\[\mathbb{E}_{\mathbf{x}_t, t, s} \left[ w(t,s) \text{MMD}^2\left(f_{t \to s}(\mathbf{x}_t, t,s), f_{r \to s}(\mathbf{x}_{r}, r,s)\right) \right]\]

where \(w(t,s)\) is a weighting function.

Sampling: Same spirit as AYF.

Closing Thoughts

The concept of a flow map offers a capable and unifying notation for summarizing the diverse landscape of diffusion distillation methods. Beyond these ODE distillation methods, an intriguing family of approaches pursues a more direct goal: training a one-step generator from the ground up by directly matching the data distribution from the teacher model.

The core question is: how can we best leverage a pre-trained teacher model to train a student that approximates the data distribution \(p_{\text{data}}\) in a single shot? With access to the teacher’s flow, several compelling strategies emerge. It becomes possible to directly match the velocity fields, minimize the \(f\)-divergence between the student and teacher output distributions, or align their respective score functions.

This leads to distinct techniques in practice. For example, adversarial distillation employs a min-max objective to align the two distributions, while other methods like IMM rely on statistical divergences like the Maximum Mean Discrepancy (MMD).

In our own work on human motion prediction, we explored this direction by using Implicit Maximum Likelihood Estimation (IMLE). IMLE is a potent, if less common, technique that aligns distributions based purely on their samples, offering a direct and elegant way to distill the teacher’s knowledge without requiring an explicit density function or a discriminator.

Diffusion distillation is a dynamic field brimming with potential. The journey from a hundred steps to a single step is not just a technical challenge but a gateway to real-time, efficient generative AI applications.